バナジウム酸化物系の科学
The
Science of Vanadium Oxide Systems
小野田雅重
Masashige
Onoda
(University
of Tsukuba)
1. はじめに
遷移金属酸化物の研究は基礎から応用に至るまで広範囲に行われており,対象物質をバナジウム酸化物系に限定しても整理することは容易ではない.ここでは著者が行っている量子スピン系(幾何学的競合系あるいはフラストレーション系),金属絶縁体転移系(相関電子系),イオンバッテリー系,そして複合結晶系に関する最近の結果を,結晶構造および電子相関(磁気,伝導特性)の観点から包括的にまとめる.一見すると全く独立した研究に感じられるかもしれないが,実は,図1に示すようにそれらの内容は相互に関連している.

図1 バナジウム酸化物系の研究例
2. 量子スピン系
物質の磁性を解析する際に有効な分子場近似は,スピンを古典的なベクトルとして,そのz成分のみを問題にする.しかし実際にはスピンSx,Sy,Szはともに演算子であり,それらの間には交換関係が成立することに注意しなければならない.またスピンのz成分と長さの比![]() は1より小さく,S = 1/2のときこの比は最小となる.これらの量子効果は,S = 1/2の場合や反強磁性の基底状態を決定する上で重要となる.
は1より小さく,S = 1/2のときこの比は最小となる.これらの量子効果は,S = 1/2の場合や反強磁性の基底状態を決定する上で重要となる.
フラストレーションのある系は量子効果の最も強く現れる系として興味深い.たとえば1次元交換結合J1−J2モデルでは,古典的にはスパイラル秩序が現れるのに対して,S = 1/2系では2量体秩序が現れる.現在,最も活発に研究されている格子はスピネル格子1)と三角格子2)である.
スピネル型MV2O4(M = Cd,Mg,Zn)では,V3+イオン(3d2;S = 1)がB席に位置し,2個の電子は縮退したt2g軌道を占有する.本系は,それぞれTc1
= 97,64.5,52 Kで立方晶からの構造転移と磁気転移,さらに低温のTc2 = 35,45,44 Kで反強磁性秩序を示す.T > Tc1における帯磁率の温度依存性は,強いフラストレーションを反映し低温領域でCurie−Weiss則から外れる.この振舞いは,高温級数展開法で決定された最近接交換相互作用Jを用いて,スピン1重項4量体を単位とする量子コンスタント結合(QCC)モデルを適用することにより説明される.このモデルの微視的理論の確立は今後の研究に委ねられるが,本系の磁気的性質を整理する際のガイドラインと考えてよいだろう.Tc1ではJahn−Teller効果により正方晶に歪み,2電子のうちの一つが優先的にdxy軌道を占めるために,Vイオンのネットワークは2種類の交換相互作用(J’,J’’)で表される(図2).CdV2O4のTc2 < T < Tc1における帯磁率の振舞いも,拡張したQCCモデルを用いて,図3の実線のように理解できる.このときの交換相互作用の大きさはdxy軌道の安定化により期待される交換相互作用の変化と定性的に一致する.すなわち,Tc1における相転移機構は,Jahn−Teller効果およびそれに伴う交換相互作用の変化に帰着される.Tc2以下での基底状態としては,2電子がdxyの他にどの軌道を占有するのか,すなわちdxz,dyz軌道を交互に占めるのか,あるいはそれらの縮退した軌道を占めるのか,で意見が分かれている.これは,Jahn−Teller型構造転移を伴わないフラストレーションが保持されたS = 1系の基底状態とともに,今後解明されるべき基本的問題である.
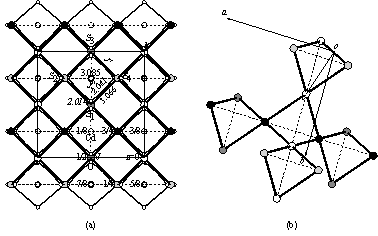
図2 CdV2O4の85 Kにおける結晶構造
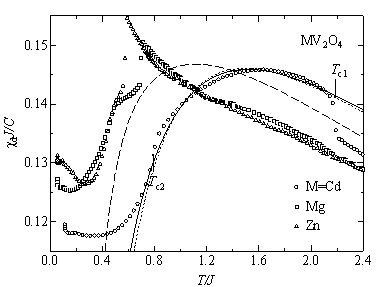
図3 MV2O4の還元スピン帯磁率
(a) 正方晶ab面への投影図.結合に添付された値はV−VおよびV−O結合長,円の値はz座標を示す.(b) 正方晶に歪んだV44面体の結合からなるVネットワーク.太線と点線は,それぞれ交換結合J’およびJ”に対応する.実(点)線は交換結合J’ = 33.5 (47.4),J” = 55.4
(29.3) Kに対する拡張QCCモデルによる計算値,破線はJ = 44 Kに対するQCCモデルによる計算値を表す.
MV2O4はAnderson型金属絶縁体転移系LixM1-xV2O4の絶縁相母物質でもある.もう一方のLiV2O4の金属性およびそれに相反するような局在的磁性は古くから知られていたが,近年,低温領域において重い電子的性質が指摘されたこともあって,さらに活発に研究が行われている.
2次元CuO2面を共通の特徴とする銅酸化物高温超伝導体の研究を契機として,梯子格子にも興味が持たれている.これはS = 1/2のHeisenberg型反強磁性1次元鎖が複数本梯子のように繋がったものを指し,1次元鎖と高温超伝導体における2次元面格子を連続的に結ぶ擬1次元的な平面格子として見てとれる.単純な1次元鎖は量子ゆらぎのため長距離反強磁性秩序を持たず,また磁気励起にギャップを持たないのに対して,高温超伝導体の母物質では長距離反強磁性秩序が存在する.一方,梯子格子の基底状態は,梯子を形成する鎖の本数で異なる.奇数本の梯子はギャップを持たないが,偶数本の場合は短距離スピン相関が強くスピン液体が基底状態となり,磁気励起に有限のギャップが存在する.梯子格子関連のバナジウム酸化物の代表としてMV2O5(M = Ca,Mg)がある3).V4+イオン(3d1;S = 1/2)のネットワークは2本脚梯子間にジグザグの相互作用も働く可能性のある系でトレリス格子と呼ばれる(次節で紹介するV6O13の結晶構造図4(b)参照).本物質の帯磁率の温度依存性はギャップの存在を示しており,それは,梯子段上の交換相互作用が大きく働くことによる2量体形成に帰着される.一方,本物質と同様のネットワークを持つNaV2O5のVイオンはV4+とV5+(3d0;S = 0)の混合原子価状態をとるが,この場合は梯子段上で分子軌道を形成するために1次元磁性を示す.本物質の基底状態がスピン1重項であることは約20年前に示唆されていたが,その後の研究により電荷局在を伴う転移であることが明らかにされている.
CaV2O5はCaVnO2n+1系の一つであり,n = 3,4も特徴的な構造および磁性を示す.トレリス格子が層状に重なった格子(図4(c))を持つδ相MxV2O5(M = Ag,Tl,Na,Sr)ブロンズでは,コメンシュレートな組成においてスピン1重項状態が現れる4).その原因はMx
= Sr0.5を除き,CaV2O5と類似の機構による.Srの場合には電荷局在による1次元的な反強磁性交替鎖の効果によって,スピン1重項となる.δ相ではV4+とV5+の混合原子価状態になることで伝導性は高くなるが,すべての組成において軌道1重項でありバンド幅も狭いため,金属的伝導は実現しない.
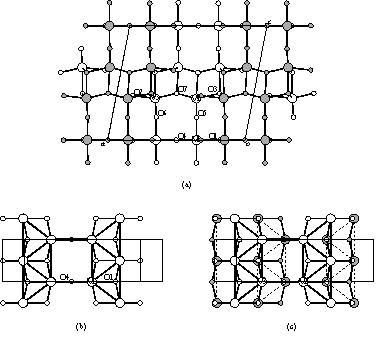
図4 V6O13の結晶構造
(a) 単斜晶ac面への投影図.空丸,実丸はy = 0,1/2の位置を示す.(b) V1トレリス格子,(c) V2,V3からなる2重トレリス格子のab面投影図.(b),(c)の太線,点線はz値が近いV−Vパスを表し,(c)の空丸,実丸はz ≃ 0.4,0.6の位置を示す.
3. 金属絶縁体転移系
ルチル型VO2およびコランダム型V2O3をはじめとして,Magnéli相VnO2n-1そしてWadsley相VnO2n+1における劇的な金属絶縁体転移現象は,高温超伝導と肩を並べる遷移金属酸化物における物性の代表例である.本節では,2節の後半で述べたトレリス格子との関連からV6O13(Wadsley相のn = 6)の物性を紹介する5).図4に示すように酸素8面体配位を持つ結晶学的に独立な3種類のV席(V1,V2,V3)が存在し,V1は単独でトレリス格子を,V2とV3は2重トレリス格子を形成し,V−O結合距離からそれらの有効価数はそれぞれ4.2,4.6,4.3と評価される.V6O13はTc ≃ 150 Kで金属絶縁体転移を示し,1次元的な電子状態によりフェルミ端が存在しない.Tc以下の絶縁体相では構造が歪み,スピンの一部が1重項状態に転移する.同時に電荷の再分布が起き,V1,V2,V3がそれぞれ(精度は不明だが)4.4,4.4,4.2になる.さらにTN ≃ 50 Kで反強磁性状態に転移する.
図5は単結晶の電気抵抗率の温度変化である.本物質の1次元伝導性を反映し,T > Tcでは,b軸方向で金属的であるのに対して,それに垂直な方向の抵抗率は温度にほぼ反比例する.前者の温度依存性は,強い反強磁性的スピンのゆらぎによる散乱機構を考えれば説明できると思われる.金属相におけるホール係数の温度依存性はb,a軸ともにR ≃ 1.1×10-6T cm3 C-1で与えられる.温度の低下に伴うホール係数の減少は単純ではなく,この振舞いが,低次元電子系における非フェルミ液体(朝永−Luttinger)効果として理解できるかどうかは今後の課題である.磁気的性質に関しては,金属相における帯磁率の強い温度依存性が,一様な電子分布に対する,バンド幅とクーロン斥力が同程度の1次元Hubbardモデルで説明されている.絶縁相の振舞いは,価数秩序を伴って2重トレリス格子上のスピンがギャップを形成し,単一格子上では3d軌道の対称性がMV2O5とは異なるために,1次元Heisenberg状態に転移すると考えればよい.
なおV6O13は1化学式あたり約6個のLiが入ることから,高容量のLiイオンバッテリーの母結晶としても注目されている.
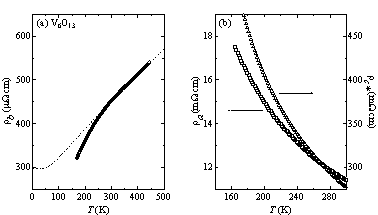
図5 V6O13単結晶の電気抵抗率
(a)
T > Tcにおけるb軸方向および(b) a,c*軸方向の結果.(a)の点線はBloch−Grüneisen機構を仮定したときの計算値.
4. イオンバッテリー系
三角格子LiCoO2やLiNiO2をはじめとするイオンバッテリー系正極活物質に関する研究は膨大である.しかし充放電過程における物質の基礎的性質を多角的に追究した例はそれほど多くはなく,バッテリーの高容量化やサイクル特性の向上は元より,多くの検討すべき課題が存在する.バナジウム酸化物系における正極活物質としてはM1+xV3O8(M = Li,Na,Ag)6, 7),3節で記したV6O13,植込み型除細動器として実用化されているAg2V4O118),そして5節で述べる複合結晶性CuxV4O11等が挙げられる.すべての物質に共通する点はLi挿入を可能にするような低次元構造を持つことであるが,代表的活物質の構造と比較するとかなり複雑である.これらの放電試料は,ほぼV4+のみからなる高密度電子系に対応し,量子スピン系あるいは相関電子系における物質探索の観点からも興味深い.但し,電気化学法やソフト化学法により得られる試料の結晶性は高くないため,物性研究が制限されることが難点である.
Li1+xV3O8を活物質とする電池の初期電位は,Li金属負極に対して約3.7 Vと低いが,民生用電池に比べ2倍以上の放電容量をもつ利点がある.図6に示すように,結晶構造は,8面体配位のVO6と歪んだピラミッド型配位のVO5からなるV3O8層がa軸方向に積まれ,その層間にある酸素8面体席に1個のLi(あるいはNa,Ag)が入る.x個のLiは同じ層間にある酸素4面体席に入る.0 ≤ x ≤ 1.5ではLi1+xV3O8型の単相(γ1相)であり,1.5 ≤ x ≤ 3ではγ1相と擬NaCl型のLi4V3O8相(γ2相)が共存し,x ≥ 3ではγ2の単相となる.共存相では平坦な充放電特性が現れる.なおMx = Ag1.229およびNa1.164の結晶構造も精密に決定され,これらを活物質にした場合における充放電特性の不可逆性機構が明らかにされている.
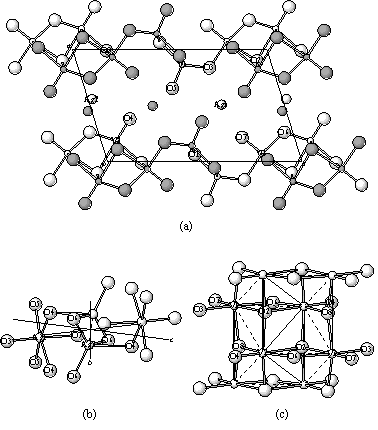
図6 Ag1.229V3O8の295 Kにおける結晶構造
(a) 単斜晶ac面への投影図.空,実丸はそれぞれy = 1/4,3/4の位置を表す.(b) Ag1のAg2の局所構造.破線はAg2−Ag2対を表す.(c) V2およびV3のネットワーク.太線と細線は等価原子位置に対する点,稜共有パス,破線は非等価位置間パスを表す.
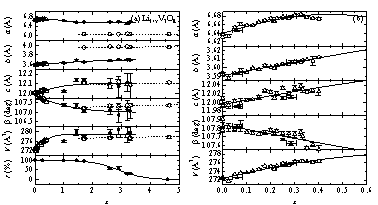
図7 Li1+xV3O8の格子定数および全体相に対するγ1相の存在比r
(a)
Li全濃度領域の結果.実,空記号は,それぞれγ1,γ2相の結果を示す.(b)
γ1相の低濃度領域における格子定数.
γ1およびγ2相の格子定数から(図7),γ1相の組成依存性に異常があることがわかる.これはγ1相におけるLi2イオン間のクーロン相互作用により結晶が不安定になり,代わって他の4面体席をLiイオンが占有するためで,それは充放電特性にも反映される.Liイオンの挿入によって生じるd電子は,γ1の低ドープ領域ではV3席を主に占有する.そこでの基底状態波動関数はdxy型(x
2 2a + c,y
2 -b)であるので,輸送現象も磁気的性質もb軸に関して1次元的になることが予想される.実際,電気抵抗率の振舞いは,b軸に垂直方向のバンド幅の大きさにも依存するが,高温領域では1次元変長ホッピング(VRH)に従い,熱電能の組成依存性は電子の嗜好的占有を反映し,非縮退状態に対するHeikes式で説明されている(図8).また帯磁率はHeisenberg型反強磁性1次元鎖から期待される極大現象を示す.
Liイオンの局所環境およびダイナミクスを知るには核磁気共鳴(NMR)が適当である.γ1相に関しては,特にMagic Angle Spinning(MAS)法により,Li2席の占有率が決定され,すべてのLi席のシフトおよびスピン格子緩和時間が求められる.この時の緩和の起源としては4重極相互作用が妥当で,通常のNMRから得られた4重極定数を用いると,相関時間はτc ≃ 7.9×10-7/T sとなる.また双極子緩和に基づく解析から,室温で10-12 cm2
s-1程度の自己拡散係数が得られている.
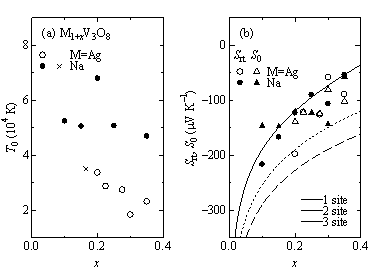
図8 Ag1+xV3O8およびNa1+xV3O8多結晶体の輸送特性
(a)
1次元VRH型エネルギーギャップT0,(b) 室温および高温極限における熱電能値(Srt,S0).曲線はHeikes式に基づく.
5. 複合結晶系
複合結晶とは,複数の基本周期も対称性も異なる部分構造が互いに貫入した結晶を指す.複数の部分構造の周期が簡単な整数比で表されなければ互いに不整合であり,構造全体は3次元の周期では記述できない.各部分構造の基本構造はそれぞれ3次元空間群の対称性をもつが,現実の構造では部分構造間の相互作用のために変位変調が生じるのが一般的であり,構造全体の記述には超空間群の利用が適当となる.
CuxV4O11はCu濃度に依存して数種の変調パターンを持つ9).その中でx
≃ 2.2は,図9に示すようにCuV4O11格子(部分構造1)とCu鎖(部分構造2)からなる複合結晶である.両構造ともに空間群Cmを持ち,b軸の格子定数はそれぞれ3.599と3.097 Åである.部分格子1上のCu1鎖はb軸方向に強い位置変調を持ち,8面体配位あるいは2種類の4面体配位をとるのに対して,部分格子2上のCu2鎖はc軸方向に強い位置変調を伴う.部分格子1のVに関する位置変調は小さく,また8面体配位に対する3d軌道の対称性から,Vネットワークは前述の2本脚梯子格子で近似することができる.Cu,Vの有効価数および電子スピン共鳴の結果から,Cu1およびCu2鎖はそれぞれCu2+(3d9;S = 1/2),Cu+(3d10;S
= 0)に近く,VはV4+,V5+の混合原子価状態をとる.
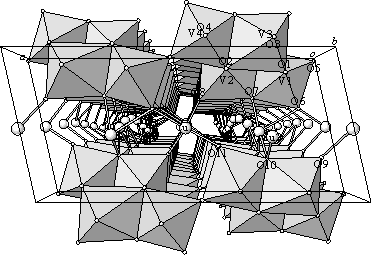
図9 Cu2.16V4O11の293 Kにおける結晶構造の単斜晶ac面への投影図
CuxV4O11の輸送特性はCu1鎖上のd電子に帰着され,電気抵抗率および熱電能はTρ1
= 120 K〜Tρ2
= 340 Kの範囲でフェルミ液体的な振舞いを示す(図10).Tρ1,Tρ2は,それぞれCuイオンの秩序化および大きな乱雑効果に起因しており,また最低温では電子間クーロン斥力によるソフトギャップが生じる.熱電能は電子相関による有効質量の増大を反映して,室温で102 μV K-1程度の値をとる.磁気的性質に関しては,340 KでVのNMRナイトシフトにギャップ的振舞いが観測されたが,これはおそらく梯子段上の2量体形成に帰着される.そのためV上のd電子の伝導および常磁性への寄与は小さいと思われる.
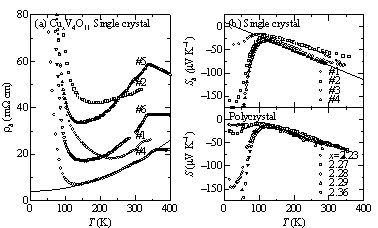
図10 CuxV4O11単結晶および多結晶の輸送特性
(a)
b軸方向の電気抵抗率.曲線はρb = 4.2 + 1.4×10-4T 2 mΩ cmを表す.(b) b軸方向および多結晶の熱電能.実線はSb = 9.6 – 0.31T
μV K-1を表す.
水分子を含む三角格子Na0.3CoO2∙1.3H2Oにおける超伝導や熱電素材への関心から,Co酸化物の研究が精力的に行われている.CuxV4O11のパワー因子は10-4 W m-1 K-2程度であるが,電気抵抗率についてはまだ改善の余地があることや不整合変調によるフォノン散乱の増強等を考慮に入れれば,新奇熱電素材の有力候補と位置づけられるであろう.
イオンバッテリー系では,Liの挿入・脱離による結晶構造の不安定性や相分離が充放電効率の低下を導くことが知られている.この問題はLiとホスト格子間に構造不整合を与えれば解決するのではないだろうか.実際CuxV4O11を活物質として充放電特性を試験したところ,1化学式あたり約4 molのLiが挿入され,またサイクル特性が高いことが明らかにされた10).このときLiはCu2+鎖近傍の間隙に位置すると考えられる.
Cu1鎖が金属的であり,V4O11が局在的であることから,CuxV4O11はLittleにより提唱された励起子型超伝導の見地からも興味深い.本複合結晶系は,Li挿入結晶の構造,物性は勿論のこと,種々の角度から検討すべき基礎的,応用的問題を含んでいる.
6. おわりに
著者によるバナジウム酸化物系に関する最近の研究内容を簡潔に述べた.酸化物研究にはいろいろなカテゴリーがあるが,今後はそれらを系統的に整理する必要があるだろう.特に最後に紹介したCuxV4O11は,量子スピン系,金属絶縁体転移系,イオンバッテリー系,複合結晶系,すべてを網羅しており興味深いが,その物性を完全に理解するには一層の努力が必要である.なおここでは触れなかったが,関連物質における最近の話題としてβ相ブロンズの圧力誘起超伝導やペロブスカイト相における軌道秩序問題等がある.
「結晶構造とマクロ物性の理解」は尽きぬ興味を我々に与えてくれている.
文献
紙数の都合上,詳細については以下の論文の引用文献を参照してほしい.
1)
M. Onoda and J. Hasegawa, J. Phys.:
Condens. Matter, 15, L95-L102 (2003).
2)
小野田雅重,長澤博,日本物理学会誌 49, 559-563 (1994).軌道秩序問題に関しては,H. F. Pen, J. van den Brink, D. I. Khomskii and G. A. Sawatzky, Phys.
Rev. Lett. 78, 1323-1326 (1998).
3)
N. Nishiguchi, M. Onoda and K. Kubo,
J. Phys.: Condens. Matter, 14, 5731-5746 (2002).
4)
M. Onoda and J. Hasegawa, J. Phys.:
Condens. Matter, 18, 2109-2123 (2006).
5)
M. Onoda, T. Ohki and Y. Uchida, J.
Phys.: Condens. Matter, 16, 7863-7871 (2004)..
6)
M. Onoda, J. Phys.: Condens. Matter, 16,
8957-8969 (2004).
7)
M. Onoda, S. Miyasaka, T. Mutoh and K.
Nichogi, J. Phys.: Condens. Matter, 17, 4057-4071 (2005).
8)
M. Onoda and K. Kanbe, J. Phys.:
Condens. Matter, 13, 6675-6686 (2001).
9)
Masashige Onoda and Mitsuko Onoda,
Phys. Rev. B 73, 104108 (2006) [7 pages].
10) 二梃木克洋,私信.