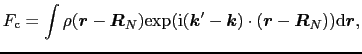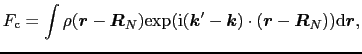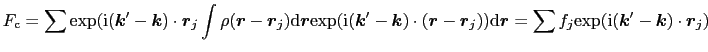結晶構造因子の計算

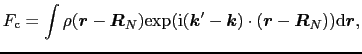$$F_{\rm c} = \int \rho(\mbox{\boldmath$r$} - \mbox{\boldmath$R$}_{... ...cdot(\mbox{\boldmath$r$} - \mbox{\boldmath$R$}_{N})){\rm d}\mbox{\boldmath$r$},$$ (1.5.26)

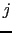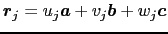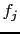
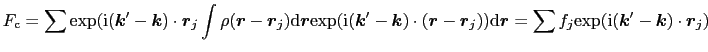単位胞内の1つの格子点 = 原点，$j$番目の原子位置： $\mbox{\boldmath$r$}_{j} = u_{j}\mbox{\boldmath$a$} + v_{j}\mbox{\boldmath$b$} + w_{j}\mbox{\boldmath$c$}$，原子構造因子 = $f_{j}$

$$F_{\rm c} = \sum {\rm exp}({\rm i}(\mbox{\boldmath$k$}' - \mbox{\... ...\rm i}(\mbox{\boldmath$k$}' - \mbox{\boldmath$k$})\cdot\mbox{\boldmath$r$}_{j})$$ (1.5.27)

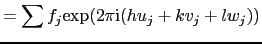$$=\sum f_{j}{\rm exp}(2\pi{\rm i}(hu_{j} + kv_{j} + lw_{j}))$$ (1.5.28)

1. 単一の原子からなる面心立方格子の場合
   $(0 0 0)$， $(0 \frac{1}{2} \frac{1}{2})$， $(\frac{1}{2} 0 \frac{1}{2})$， $(\frac{1}{2} \frac{1}{2} 0)$
   
   

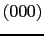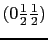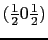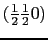
   $$F_{\rm c} = f[1 + {\rm exp}({\rm i}\pi(k + l)) + {\rm exp}({\rm i}\pi(h + l)) + {\rm exp}({\rm i}\pi(k + h))],$$ (1.5.29)

   
   

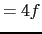
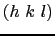$= 4f$ $(h\ k\ l)$のすべてが偶数か，奇数のとき
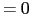
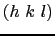$= 0$ $(h\ k\ l)$のうち一つだけが偶数か奇数のとき
現実には複数の元素からなる数多くの化合物が存在する．構造解析は複雑であるが，その結果得られる情報は，直接目に訴えるものであり，その物質の性質を研究していく上で大変貴重な情報になる．
現実の物質は，種々の様式の凝集機構によって固体を形成し，電子状態にも種々の形態が存在する．
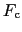$F_{\rm c}$の完全な知識，結合距離解析→ 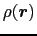$\rho(\mbox{\boldmath$r$})$，電子状態，等の決定