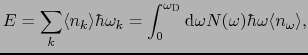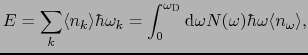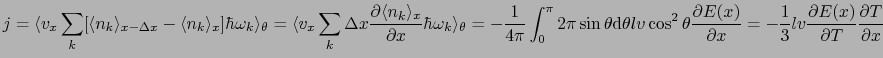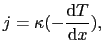: 散乱
: 結晶格子の比熱と熱伝導度
: デバイモデル
目次
結晶の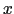 方向の両端の温度
方向の両端の温度 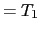 ,
,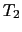 ,温度傾斜
,温度傾斜
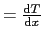
(3-6)式の拡張
点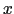 の温度
の温度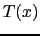 で平均をとったフォノン系の分布
で平均をとったフォノン系の分布
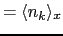 ,エネルギー密度
,エネルギー密度 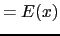
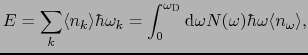 |
|
|
(2.3.41) |
フォノンの速さ 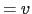 ,平均自由時間
,平均自由時間 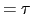 ,平均自由行路
,平均自由行路 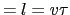
あるモードにあるフォノンが衝突なしに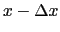 から
から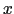 に来たとする.2つの温度は異なるため平衡分布が異なるから,運ばれた余分のエネルギーは
に来たとする.2つの温度は異なるため平衡分布が異なるから,運ばれた余分のエネルギーは
![$\displaystyle [\langle n_{k}\rangle_{x - \Delta x} - \langle n_{k}\rangle_{x}]\hbar\omega_{k},$](img238.png) |
|
|
(2.3.42) |
フォノンはあらゆる方向に進むから,
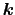 と
と
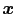 軸のなす角を
軸のなす角を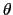 とし,
とし,
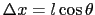 とおくと,熱流密度は
とおくと,熱流密度は
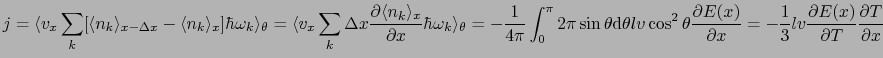 |
|
|
(2.3.43) |
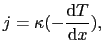 |
|
|
(2.3.44) |
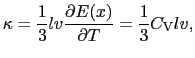 |
|
|
(2.3.45) |
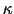 :熱伝導度,
:熱伝導度,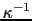 :熱抵抗
:熱抵抗
Masashige Onoda
平成18年4月7日