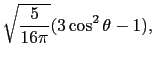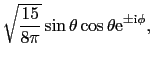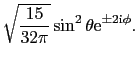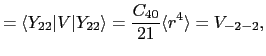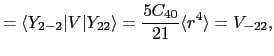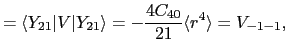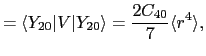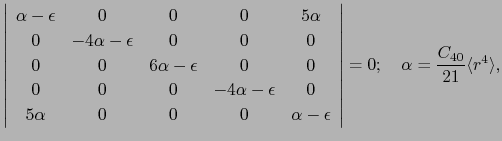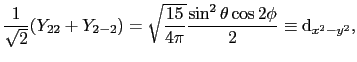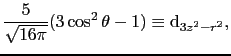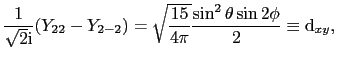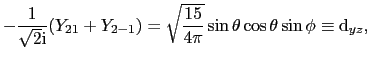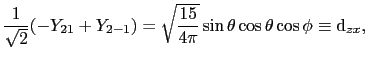: スピンハミルトニアン
: 磁性
: 軌道常磁性
目次
(3d)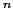 電子が結晶中にあると結晶電場によるエネルギー準位の分裂が生じる.イオン結合的結晶を採用して,磁性イオン上の電子が周りの正・負のイオンから受ける電場を考える.結晶の中の各イオンの位置を
電子が結晶中にあると結晶電場によるエネルギー準位の分裂が生じる.イオン結合的結晶を採用して,磁性イオン上の電子が周りの正・負のイオンから受ける電場を考える.結晶の中の各イオンの位置を
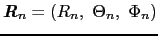 ,電荷を
,電荷を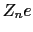 ,磁性原子の周りの電子の座標を
,磁性原子の周りの電子の座標を
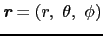 とおくと,電子の受ける静電エネルギーは
とおくと,電子の受ける静電エネルギーは
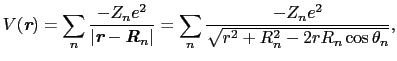 |
|
|
(6.7.67) |
と書ける.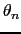 は
は
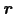 と
と
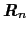 の作る角度である.電子は磁性イオンの近くに束縛されていると考え
の作る角度である.電子は磁性イオンの近くに束縛されていると考え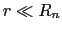 とすると数学公式により,
とすると数学公式により,
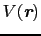 はルジャンドル関数
はルジャンドル関数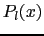 を用いて
を用いて
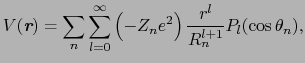 |
|
|
(6.7.68) |
と書かれる.ここで
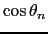 は,電子とイオンの座標で書くことができる.
は,電子とイオンの座標で書くことができる.
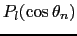 は,さらにルジャンドル陪関数
は,さらにルジャンドル陪関数
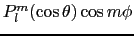 を用いて
を用いて
と書けるので
![$\displaystyle V(\mbox{\bfseries\itshape {r}}) = \sum_{l = 0}^{\infty}\sum_{m = ...
...a)\left\{
\begin{array}{ll}
\cos m\phi\\ [0.2cm]
\sin m\phi
\end{array}\right.$](img992.png) |
|
|
(6.7.70) |
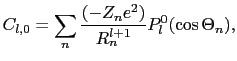 |
|
|
(6.7.71) |
![$\displaystyle C_{l, m} = \sum_{n}{(-Z_{n}e^{2}) \over{R_{n}^{l + 1}}}\cdot2{(l ...
...{
\begin{array}{ll}
\cos m\Phi_{n}\\ [0.2cm]
\sin m\Phi_{n}
\end{array}\right.$](img994.png) |
|
|
(6.7.72) |
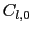 ,
,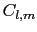 を求めるには結晶の原子座標と
を求めるには結晶の原子座標と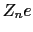 を与えて,
を与えて,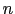 に対する和を計算する必要がある.与えられた結晶に対して,すべての
に対する和を計算する必要がある.与えられた結晶に対して,すべての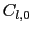 ,
,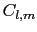 が必要ではない.それは結晶電場によるエネルギーは
が必要ではない.それは結晶電場によるエネルギーは
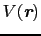 と同じ形のルジャンドル陪関数を含む波動関数
と同じ形のルジャンドル陪関数を含む波動関数
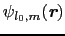 によって
によって
のように3つの球面関数の積の積分として与えられるからである.
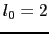 のd,
のd,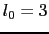 のf波動関数をとると,
のf波動関数をとると,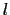 と
と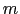 に対する格子和は以下のように限定される.
に対する格子和は以下のように限定される.
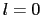 の電場に対する格子和は電子軌道
の電場に対する格子和は電子軌道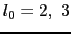 に対して等方的(丸い)であるので,そのエネルギー準位には影響を与えない.この
に対して等方的(丸い)であるので,そのエネルギー準位には影響を与えない.この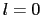 の格子和はイオン結晶の結合エネルギーを与えるマーデルングエネルギーそのものである.
の格子和はイオン結晶の結合エネルギーを与えるマーデルングエネルギーそのものである.
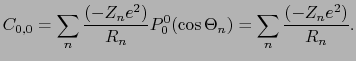 |
|
|
(6.7.73) |
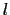 が奇数の電場部分は,波動関数の積の偶関数性によって自動的に消失するので,この項は必要ない.
が奇数の電場部分は,波動関数の積の偶関数性によって自動的に消失するので,この項は必要ない.
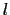 が偶数の場合,dとf波動関数に影響を及ぼす
が偶数の場合,dとf波動関数に影響を及ぼす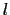 ,
,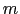 には上限があって,
には上限があって,
 の和をとる必要はない.その上限はd関数に対しては
の和をとる必要はない.その上限はd関数に対しては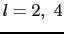 と
と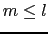 ,f関数に対しては
,f関数に対しては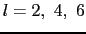 と
と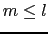 だけである.それは,
だけである.それは,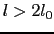 に対する積分は消失するからである.
に対する積分は消失するからである.
- こうして選び出された
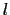 ,
,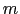 は,とりあげている結晶の対称性(厳密には着目する磁性イオンの周りのイオン配位の対称性)によってさらにその数が限られる.
は,とりあげている結晶の対称性(厳密には着目する磁性イオンの周りのイオン配位の対称性)によってさらにその数が限られる.
d波動関数が立方晶の結晶電場に置かれた場合を考える.中心の磁性イオンはd電子1個のみをもつと考える.周りのイオンは
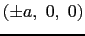 ,
,
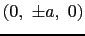 ,
,
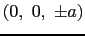 に電荷
に電荷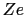 をもつ.
をもつ.
結晶場の対称性から
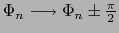 の操作で不変なものとして
の操作で不変なものとして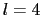 ,
,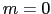 と
と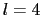 ,
,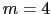 だけが残り,さらにイオン1,2,イオン3,4のように反対向きのイオンについての和をとる場合に,
だけが残り,さらにイオン1,2,イオン3,4のように反対向きのイオンについての和をとる場合に,
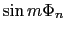 の項は打ち消しあう.
の項は打ち消しあう.
したがって
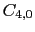 の内容を書かなかったのは,点電荷模型が成立しない場合にも使う目的のためである.
の内容を書かなかったのは,点電荷模型が成立しない場合にも使う目的のためである.
d電子が1個の場合とすれば,自由イオンの波動関数は球関数
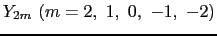 で与えられる.
で与えられる.
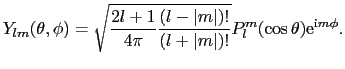 |
|
|
(6.7.75) |
これらの関数を用いれば
を得る.したがって固有値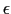 は
は
より
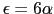 (2重縮退),
(2重縮退),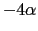 (3重縮退)となる.固有関数は,
(3重縮退)となる.固有関数は,
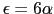 のとき
のとき
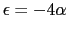 のとき
のとき
となる.




: スピンハミルトニアン
: 磁性
: 軌道常磁性
目次
Masashige Onoda
平成18年4月7日
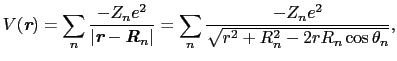
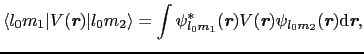
![]() のd,
のd,![]() のf波動関数をとると,
のf波動関数をとると,![]() と
と![]() に対する格子和は以下のように限定される.
に対する格子和は以下のように限定される.
![]() ,
,
![]() ,
,
![]() に電荷
に電荷![]() をもつ.
をもつ.
![]() の操作で不変なものとして
の操作で不変なものとして![]() ,
,![]() と
と![]() ,
,![]() だけが残り,さらにイオン1,2,イオン3,4のように反対向きのイオンについての和をとる場合に,
だけが残り,さらにイオン1,2,イオン3,4のように反対向きのイオンについての和をとる場合に,
![]() の項は打ち消しあう.
の項は打ち消しあう.
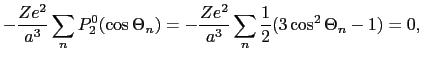
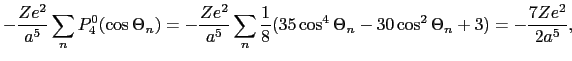
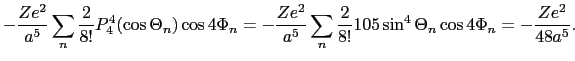
![]() で与えられる.
で与えられる.