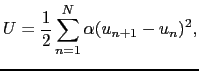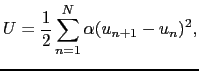: II(95B)
: 演習問題
: 演習問題
目次
- 固体の凝集機構の中から3つを,それらの代表的物質例とともに挙げて簡潔に説明せよ.【
 点】
点】
- 格子定数
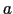 の単純立方格子,体心立方格子,面心立方格子の諸性質をまとめよう.下表の空欄ア〜ケを満たせ.【
の単純立方格子,体心立方格子,面心立方格子の諸性質をまとめよう.下表の空欄ア〜ケを満たせ.【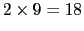 点】
点】
表 8.1:
単純立方格子,体心立方格子,面心立方格子の諸性質
| |
単純立方格子 |
体心立方格子 |
面心立方格子 |
| 通常の単位格子の体積 |
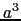 |
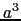 |
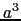 |
| 単位格子あたりの格子点数 |
ア |
エ |
キ |
| 最近接格子点数 |
イ |
オ |
ク |
| 最近接格子点間距離 |
ウ |
カ |
ケ |
- 逆格子ベクトル
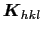 の持つ以下の性質を証明せよ.【
の持つ以下の性質を証明せよ.【
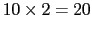 点】
点】
- 逆格子の原点から,
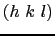 の座標の点に引いたベクトル
の座標の点に引いたベクトル
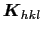 は,ミラー指数
は,ミラー指数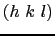 の格子面に垂直である.
の格子面に垂直である.
-
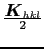 の長さは
の長さは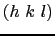 面の面間隔の逆数に等しい.
面の面間隔の逆数に等しい.
- 単位格子あたり質量
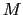 の原子を1個もつ,平均の格子間隔
の原子を1個もつ,平均の格子間隔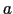 ,長さ
,長さ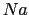 の1次元鎖がある.ここで最隣接原子間にのみ力が働き,鎖方向の原子の変位
の1次元鎖がある.ここで最隣接原子間にのみ力が働き,鎖方向の原子の変位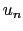 に対して,原子間相互作用は以下の調和振動子型ポテンシャルエネルギーで記述できるとする.
に対して,原子間相互作用は以下の調和振動子型ポテンシャルエネルギーで記述できるとする.
但し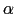 は力の定数であり,
は力の定数であり,
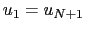 とする.このときの格子振動の分散を求めて,図示せよ.【
とする.このときの格子振動の分散を求めて,図示せよ.【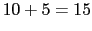 点】
点】
- 2次元自由電子系の状態密度を,スピンの自由度を考慮に入れて求め,そのエネルギー依存性について述べよ.但し必要であれば,系の面積を
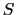 ,電子の質量を
,電子の質量を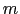 ,プランク定数を
,プランク定数を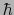 (
(
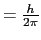 )とせよ.【
)とせよ.【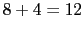 点】
点】
- 自由電子モデルにおいて,総数
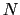 個の電子を収容したときのフェルミ波数
個の電子を収容したときのフェルミ波数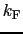 とフェルミエネルギー
とフェルミエネルギー
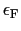 を,スピンの自由度を考慮に入れて求めよ.但し必要であれば,系の体積を
を,スピンの自由度を考慮に入れて求めよ.但し必要であれば,系の体積を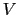 ,電子の質量を
,電子の質量を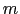 ,プランク定数を
,プランク定数を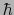 (
(
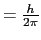 )とせよ.【
)とせよ.【
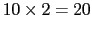 点】
点】
Masashige Onoda
平成18年4月7日
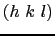 の座標の点に引いたベクトル
の座標の点に引いたベクトル
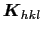 は,ミラー指数
は,ミラー指数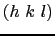 の格子面に垂直である.
の格子面に垂直である.
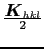 の長さは
の長さは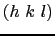 面の面間隔の逆数に等しい.
面の面間隔の逆数に等しい.