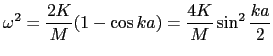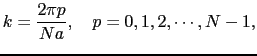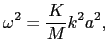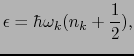: 2種類の原子からなる1次元格子
: 格子振動とフォノン
: 格子振動とフォノン
目次
原子の質量 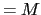
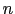 番目の原子の平衡点からの変位
番目の原子の平衡点からの変位 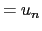
変位に対する復元力 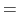 最隣接原子からのみ
調和振動子型:
最隣接原子からのみ
調和振動子型:
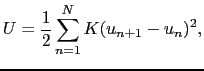 |
|
|
(2.1.1) |
変位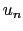 の運動方程式:
の運動方程式:
![$\displaystyle M{{\rm d}^{2}u_{n} \over{{\rm d}t^{2}}} = -{\partial U \over{\par...
...{n})^{2} + {1 \over{2}}K(u_{n} - u_{n-1})^{2}] = K(u_{n+1} + u_{n-1} - 2u_{n}),$](img152.png) |
|
|
(2.1.2) |
ここで,解が波であることを予想して
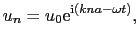 |
|
|
(2.1.3) |
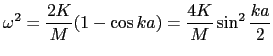 |
|
|
(2.1.4) |
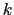 のとり得る範囲は周期的境界条件より決定する.
のとり得る範囲は周期的境界条件より決定する.
系の長さ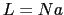 ,変位
,変位
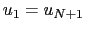
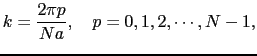 |
|
|
(2.1.5) |
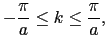 |
|
|
(2.1.6) |
長波長の格子振動→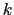 で展開
で展開
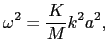 |
|
|
(2.1.7) |
上で与えられる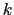 に対し,調和振動子として格子振動を量子化して,
に対し,調和振動子として格子振動を量子化して,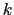 の格子振動のエネルギーを
の格子振動のエネルギーを
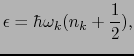 |
|
|
(2.1.8) |
とおくとき,格子振動をフォノンとよぶ.




: 2種類の原子からなる1次元格子
: 格子振動とフォノン
: 格子振動とフォノン
目次
Masashige Onoda
平成18年4月7日
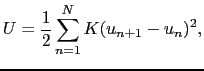
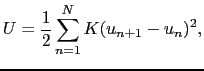
![$\displaystyle M{{\rm d}^{2}u_{n} \over{{\rm d}t^{2}}} = -{\partial U \over{\par...
...{n})^{2} + {1 \over{2}}K(u_{n} - u_{n-1})^{2}] = K(u_{n+1} + u_{n-1} - 2u_{n}),$](img152.png)