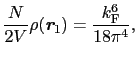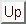


: フェルミ統計
: 金属,半導体
: 金属,半導体
目次
電子は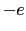 の電荷をもち,スピン
の電荷をもち,スピン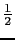 のフェルミ統計に従う粒子である.多電子系に対しては一般的には次の形にシュレーディンガー方程式が書き表される.
のフェルミ統計に従う粒子である.多電子系に対しては一般的には次の形にシュレーディンガー方程式が書き表される.
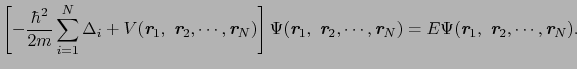 |
|
|
(4.1.1) |
この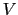 の中には電子間のクーロン相互作用も含まれている.(4.1.1)式を
の中には電子間のクーロン相互作用も含まれている.(4.1.1)式を
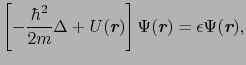 |
|
|
|
| |
|
|
(4.1.2) |
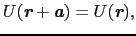 |
|
|
|
のように1体化することにどのような背景があるか,また,フェルミ統計の性質が多電子系についてどのような影響を与えるか,について考えよう.
いま1電子関数の空間部分を
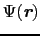 ,スピンの状態を
,スピンの状態を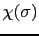 (ただし
(ただし
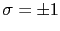 )で表す.スピンは
)で表す.スピンは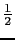 の大きさであるから,量子化軸について上向きスピンの状態なら,
の大きさであるから,量子化軸について上向きスピンの状態なら,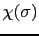 を
を
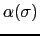 と書き,
と書き,
下向きの状態なら
と書く.したがって,
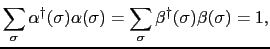 |
|
|
|
| |
|
|
(4.1.3) |
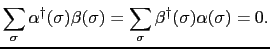 |
|
|
|
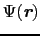 と
と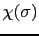 をまとめて1電子関数を
をまとめて1電子関数を
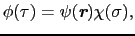 |
|
|
(4.1.4) |
と表す.
2電子系であれば,
である.
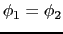 とすると
とすると
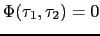 となり,1つの固有状態にはただ1つの粒子しか入れない.これがパウリの原理である.考えている系に
となり,1つの固有状態にはただ1つの粒子しか入れない.これがパウリの原理である.考えている系に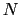 個の電子があるとし,それらが
個の電子があるとし,それらが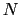 個の与えられた状態を占めているとすると,全電子の波動関数は,
個の与えられた状態を占めているとすると,全電子の波動関数は,
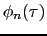 は規格直交系であるとする.
は規格直交系であるとする.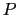 は
は
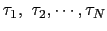 についての置換を表し,
についての置換を表し,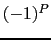 はその置換が偶であれば
はその置換が偶であれば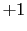 ,奇であれば
,奇であれば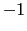 をとると約束する.(4.1.5)式はスレーターの行列式と呼ばれる.
をとると約束する.(4.1.5)式はスレーターの行列式と呼ばれる.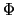 はすべての座標(スピン座標も含めて)で積分すれば1に規格化されている.
はすべての座標(スピン座標も含めて)で積分すれば1に規格化されている.
この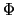 で表される状態の中で,特定の2つの電子,たとえば
で表される状態の中で,特定の2つの電子,たとえば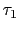 と
と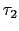 で代表される電子がどのような相関をもっているかを調べるために,
で代表される電子がどのような相関をもっているかを調べるために,
を考える.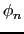 どうしは互いに直交するから,
どうしは互いに直交するから,
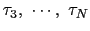 の積分で残るためには,
の積分で残るためには,
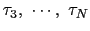 の各座標を含む
の各座標を含む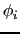 が
が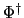 と
と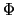 の中で同一のものでなければならない(たとえば
の中で同一のものでなければならない(たとえば
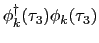 のように).したがって,
のように).したがって,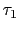 ,
,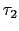 を含む
を含む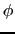 は
は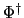 と
と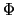 とで同じ対のものになり,その対を指定したときに,その他の座標
とで同じ対のものになり,その対を指定したときに,その他の座標
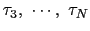 を残りの
を残りの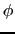 へばらまく仕方は
へばらまく仕方は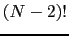 あるから
あるから
となる.これに(4.1.4)式を代入し,スピン座標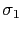 ,
,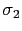 で和をとると,(4.1.4)式によって第2項は
で和をとると,(4.1.4)式によって第2項は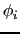 と
と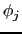 とが同一のスピン状態のときだけ残るから
とが同一のスピン状態のときだけ残るから
この第2項を交換項と呼ぶ.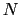 は十分大きいとして,
は十分大きいとして,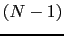 は
は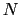 においてよい.(4.1.6)式を
においてよい.(4.1.6)式を
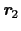 で積分すると,着目した
で積分すると,着目した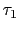 の電子が
の電子が
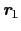 に存在する確率が得られる:
に存在する確率が得られる:
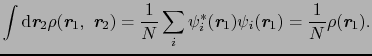 |
|
|
(4.1.7) |
(4.1.6)式の第2項は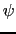 の直交性により消えた.個々の電子の区別はつかないという量子力学の原則から,
の直交性により消えた.個々の電子の区別はつかないという量子力学の原則から,
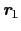 に1つの電子が実際存在するときに,
に1つの電子が実際存在するときに,
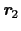 に残りの
に残りの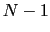 個の電子のどれかがある確率は,(4.1.6),(4.1.7)式を用いて,
個の電子のどれかがある確率は,(4.1.6),(4.1.7)式を用いて,
ここで
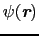 として自由電子の波動関数
として自由電子の波動関数
を使って
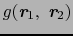 を考察する.(4.1.7)式により
を考察する.(4.1.7)式により
である.いま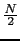 個ずつの電子が上向きおよび下向きスピンの電子とすると,
個ずつの電子が上向きおよび下向きスピンの電子とすると,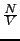 のうち
のうち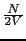 がそれぞれの電子からの寄与である.これらそれぞれのスピンの電子が,どちらも
がそれぞれの電子からの寄与である.これらそれぞれのスピンの電子が,どちらも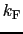 のフェルミ波数ベクトルをもつとすると,
のフェルミ波数ベクトルをもつとすると,
である.ここで
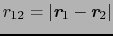 である.
である.
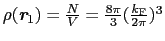 を用いると,
を用いると,
であるから
と表すことができる.
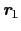 に1つの電子があるときに
に1つの電子があるときに
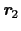 に残りの
に残りの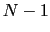 個の電子のどれかがある確率は,
個の電子のどれかがある確率は,
![$\displaystyle \frac{g(\mbox{\bfseries\itshape {r}}_{1},\ \mbox{\bfseries\itshap...
...\sin k_{\rm F}r_{12} - k_{\rm F}r_{12}\cos k_{\rm F}r_{12})\right]^{2}\right\}.$](img538.png) |
|
|
(4.1.9) |
右辺の第1項は互いに反対のスピンをもつ電子からの寄与であり,第2項は同じスピンをもつ電子からの寄与である.逆スピンの電子どうしは互いに近づけるが,同一スピンの電子どうしは,パウリの排他率が効いて,互いに同一の空間を占めることができない.この同じスピンの電子を退けてできた中心付近の穴が,最初に
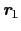 におくために取り出した1つの電子の欠損部分である.
におくために取り出した1つの電子の欠損部分である.



: フェルミ統計
: 金属,半導体
: 金属,半導体
目次
Masashige Onoda
平成18年4月7日
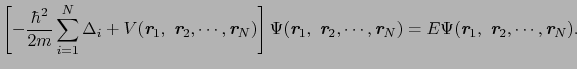
![]() ,スピンの状態を
,スピンの状態を![]() (ただし
(ただし
![]() )で表す.スピンは
)で表す.スピンは![]() の大きさであるから,量子化軸について上向きスピンの状態なら,
の大きさであるから,量子化軸について上向きスピンの状態なら,![]() を
を
![]() と書き,
と書き,
![$\displaystyle \Phi(\tau_{1}, \tau_{2}) = \frac{1}{\sqrt{2!}}
\left\vert \begin{...
...{1}(\tau_{1})\phi_{2}(\tau_{2}) - \phi_{1}(\tau_{2})\phi_{2}(\tau_{1}) \right],$](img483.png)
![$\displaystyle \Phi(\tau_{2}, \tau_{1}) = \frac{1}{\sqrt{2!}}\left[ \phi_{1}(\ta...
...1}) - \phi_{1}(\tau_{1})\phi_{2}(\tau_{2}) \right] = -\Phi(\tau_{1}, \tau_{2}),$](img484.png)
![]() で表される状態の中で,特定の2つの電子,たとえば
で表される状態の中で,特定の2つの電子,たとえば![]() と
と![]() で代表される電子がどのような相関をもっているかを調べるために,
で代表される電子がどのような相関をもっているかを調べるために,
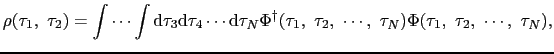
![$\displaystyle \rho(\tau_{1},\ \tau_{2}) = \frac{(N-2)!}{N!}\sum_{ij}\left[\phi_...
...\tau_{1})\phi^{\dag }_{i}(\tau_{2})\phi_{i}(\tau_{1})\phi_{j}(\tau_{2})\right],$](img505.png)
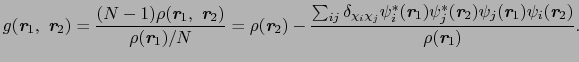
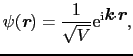
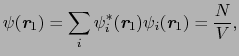
![$\displaystyle \sum_{i, j}\delta_{\chi_{i}\chi_{j}}\psi_{i}^{*}(\mbox{\bfseries\...
...2}^{3}}(\sin k_{\rm F}r_{12} - k_{\rm F}r_{12}\cos k_{\rm F}r_{12})\right]^{2},$](img530.png)