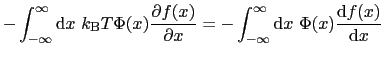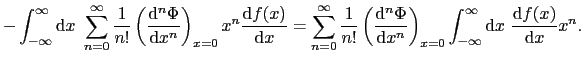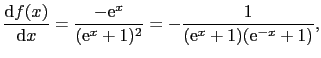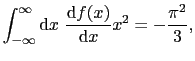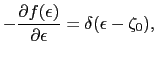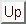


: 輸送現象
: 金属,半導体
: 電子相関
目次
金属中の伝導電子はプラズマ振動のような高いエネルギーに関係した現象を考えない限り,あるいは,低い密度の電子ガスを考えない限り,互いに独立な粒子として扱うことが許されるので,以下主としてこのような描像で電子系の性質を理解することにしよう.
原子系が温度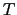 で平衡状態にあるとすると,エネルギーが
で平衡状態にあるとすると,エネルギーが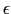 であるような1電子の量子状態にある統計的な確率はフェルミ分布関数で与えられる.
であるような1電子の量子状態にある統計的な確率はフェルミ分布関数で与えられる.
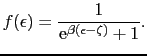 |
|
|
(4.2.10) |
化学ポテンシャル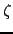 は原子の総数
は原子の総数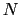 を正しく与えるように
を正しく与えるように
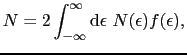 |
|
|
(4.2.11) |
を通して決められる.係数の2はスピンの自由度によるものであり,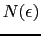 は電子の状態密度である.
は電子の状態密度である.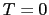 [K]では,
[K]では,
であり,フェルミエネルギー
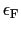 以下のすべての状態が電子で占められている.
以下のすべての状態が電子で占められている.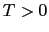 [K]では
[K]では
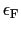 付近の
付近の
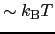 の範囲にわたって上の形が崩れる.
の範囲にわたって上の形が崩れる.
温度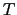 での電子系の性質を調べるときには,
での電子系の性質を調べるときには,
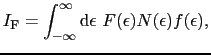 |
|
|
(4.2.12) |
の積分が必要になる.たとえば
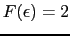 とすると(4.2.2)式となり,
とすると(4.2.2)式となり,
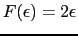 とおくと,電子系のエネルギーが得られる.一度,部分積分すると,
とおくと,電子系のエネルギーが得られる.一度,部分積分すると,
となる.ここで電子の状態があるのは有限の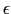 の領域だけであるので
の領域だけであるので
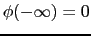 を用いた.
を用いた.
いま
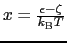 と変数変換して
と変数変換して
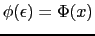 と書き,
と書き,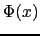 を
を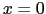 の周りでテイラー展開する.
の周りでテイラー展開する.
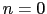 の項の積分は
の項の積分は
![$\Bigl [ f(x) \Bigr ]_{-\infty}^{\infty} = \Bigl [ \frac{1}{{\rm e}^{x}+1} \Bigr ]_{-\infty}^{\infty} = -1$](img566.png) であり,また
であり,また
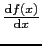 は
は
となり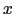 の偶関数であるから
の偶関数であるから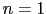 の項は消える.
の項は消える.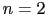 の項の積分は
の項の積分は
となるから
が得られる.特に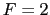 とおくと
とおくと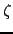 を決める式は,
を決める式は,
また(4.2.5)式と(4.2.5)式を比べて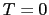 [K]では
[K]では
という等式が成り立つことがわかる.自由電子の状態密度
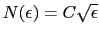 を入れると,(4.2.6)式は
を入れると,(4.2.6)式は



: 輸送現象
: 金属,半導体
: 電子相関
目次
Masashige Onoda
平成18年4月7日
![]() で平衡状態にあるとすると,エネルギーが
で平衡状態にあるとすると,エネルギーが![]() であるような1電子の量子状態にある統計的な確率はフェルミ分布関数で与えられる.
であるような1電子の量子状態にある統計的な確率はフェルミ分布関数で与えられる.
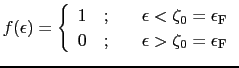
![]() での電子系の性質を調べるときには,
での電子系の性質を調べるときには,
![]() と変数変換して
と変数変換して
![]() と書き,
と書き,![]() を
を![]() の周りでテイラー展開する.
の周りでテイラー展開する.