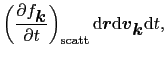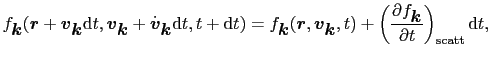: 電気伝導度
: 輸送現象
: 輸送現象
目次
金属や半導体は電気の導体である.それらの抵抗率は常温において,通常の金属で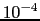 〜
〜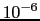
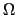 cm,良質のSiやGeで
cm,良質のSiやGeで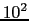 〜
〜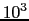
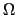 cmの程度である.電気抵抗の原因としては,結晶の中のポテンシャル場が不純物とか格子振動のために周期性を失って,ブロッホ電子を散乱することからおこる.
cmの程度である.電気抵抗の原因としては,結晶の中のポテンシャル場が不純物とか格子振動のために周期性を失って,ブロッホ電子を散乱することからおこる.
簡単な考察として,伝導帯にある電子を自由な電子として古典的なモデルを考えてみよう.電子は外から加えた電場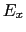 で加速されると同時に,その運動を妨げる抵抗力が働いて,
で加速されると同時に,その運動を妨げる抵抗力が働いて,
という運動方程式で記述されるとする(電子の電荷は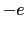 とする).この定常解は
とする).この定常解は
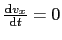 より
より
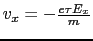 であるから,
であるから,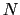 電子系の示す電気伝導度は,
電子系の示す電気伝導度は,
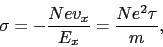 |
(5.1.1) |
で与えられる.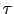 を緩和時間とよぶ.この古典的なモデルで不満足な点は,電子に対してフェルミ統計を考慮していないこと,
を緩和時間とよぶ.この古典的なモデルで不満足な点は,電子に対してフェルミ統計を考慮していないこと,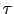 に明確な描像が与えられていないことである.
に明確な描像が与えられていないことである.
これまで扱ったフェルミ分布関数
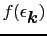 は外場のない系の平衡状態にある分布関数であり,それを改めて
は外場のない系の平衡状態にある分布関数であり,それを改めて
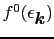 と書くことにする.外から電場
と書くことにする.外から電場
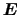 ,磁場
,磁場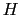 を加えたとすると,その分布は
を加えたとすると,その分布は
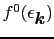 から歪むので,
から歪むので,
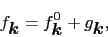 |
(5.1.2) |
と書く.外場によって電子に働く力は
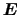 による力および
による力および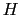 によるローレンツ力である.したがって運動方程式は,
によるローレンツ力である.したがって運動方程式は,
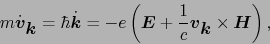 |
(5.1.3) |
であり,これは電子の状態に依存する.これに対応して新しい分布関数を
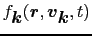 と書く.時刻
と書く.時刻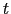 に
に
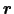 の付近d
の付近d
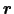 の体積要素および
の体積要素および
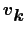 のまわりの速度空間における体積要素d
のまわりの速度空間における体積要素d
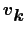 にある電子
にある電子
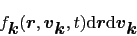 |
(5.1.4) |
は,もし電子が障害物による散乱を起さないとすれば,時刻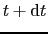 においては
においては
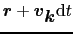 の位置に移り,
の位置に移り,
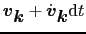 の速度をもつので,
の速度をもつので,
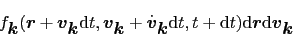 |
(5.1.5) |
で表される.
この他に電子の自由な加速を妨げる散乱によってd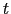 の間にd
の間にd
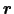 d
d
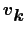 に飛び込んできたり,そこから飛び出していく電子を
に飛び込んできたり,そこから飛び出していく電子を
と書くと,(5.1.4),(5.1.5)式とあわせて
が得られる.すなわち,
これをボルツマン方程式とよぶ.
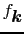 は外場の下での新しい定常状態の分布関数とすると,(5.1.6)式での第3項を落とし,(5.1.3)式を使って次の方程式を充たすことになる.
は外場の下での新しい定常状態の分布関数とすると,(5.1.6)式での第3項を落とし,(5.1.3)式を使って次の方程式を充たすことになる.
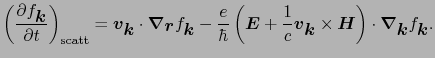 |
|
|
(5.1.7) |
もし外場が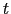 とともに変化するときには,(5.1.6)式の第3項は残しておかなければならない.
とともに変化するときには,(5.1.6)式の第3項は残しておかなければならない.




: 電気伝導度
: 輸送現象
: 輸送現象
目次
Masashige Onoda
平成18年4月7日
![]() で加速されると同時に,その運動を妨げる抵抗力が働いて,
で加速されると同時に,その運動を妨げる抵抗力が働いて,
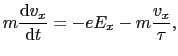
![]() は外場のない系の平衡状態にある分布関数であり,それを改めて
は外場のない系の平衡状態にある分布関数であり,それを改めて
![]() と書くことにする.外から電場
と書くことにする.外から電場
![]() ,磁場
,磁場![]() を加えたとすると,その分布は
を加えたとすると,その分布は
![]() から歪むので,
から歪むので,
![]() の間にd
の間にd
![]() d
d
![]() に飛び込んできたり,そこから飛び出していく電子を
に飛び込んできたり,そこから飛び出していく電子を