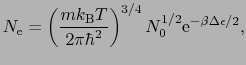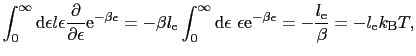: 緩和時間
: 輸送現象
: ボルツマン方程式
目次
(5.1.7)式において外場は
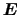 のみとし,
のみとし,
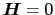 とおく.(5.1.7)式の左辺に関しては,電子の散乱過程の詳細を問題にしないで,単に
とおく.(5.1.7)式の左辺に関しては,電子の散乱過程の詳細を問題にしないで,単に
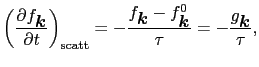 |
|
|
(5.2.8) |
とおく.
場所
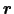 による不均一がないときは,(5.1.7)と(5.2.1)式より,
による不均一がないときは,(5.1.7)と(5.2.1)式より,
と書ける.ここで,
であるので,
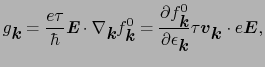 |
|
|
(5.2.9) |
が得られる.ただし,
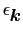 は外場を加える前のブロッホ状態のエネルギー固有値である.こうして電流は
は外場を加える前のブロッホ状態のエネルギー固有値である.こうして電流は
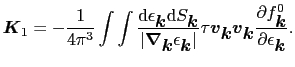 |
|
|
(5.2.11) |
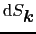 は
は
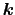 空間での
空間での
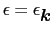 の値の面上の面素片を表す.
の値の面上の面素片を表す.
電気伝導度テンソル
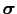 は
は
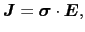 |
|
|
(5.2.12) |
で表される.簡単のために系は等方的であるとし,
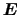 の方向を
の方向を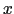 方向にとると,
方向にとると,
ここで
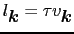 であり,これを平均自由行路とよぶ.(5.2.6)式の積分は
であり,これを平均自由行路とよぶ.(5.2.6)式の積分は
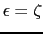 の面上で行う.
の面上で行う.
(5.2.6)式における積分はフェルミ面上での積分であるから,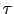 または
または
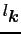 は
は
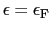 での値と理解して
での値と理解して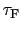 または
または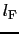 と表すと,(5.2.6)式は
と表すと,(5.2.6)式は
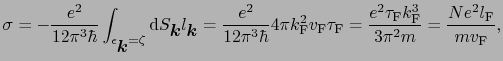 |
|
|
(5.2.14) |
となり,古典的なモデルから得られた(5.1.1)式と同じ表式になる.そこでの結果との大きな違いは,電気伝導に関与しているのはフェルミ面付近の電子であることである.
半導体のようにフェルミ縮退していない電気伝導度について考える.このときには,
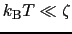 は成り立たない.
は成り立たない.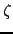 は伝導帯の底より下にあるから,伝導帯にある電子はボルツマン分布
は伝導帯の底より下にあるから,伝導帯にある電子はボルツマン分布
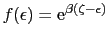 で与えられ,その電子数は
で与えられ,その電子数は
で与えられる.不純物を含んだN型半導体の場合を考えると化学ポテンシャル
(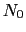 :不純物原子数;
:不純物原子数;
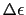 :不純物準位-伝導帯底間ギャップ)および伝導帯にある電子数
:不純物準位-伝導帯底間ギャップ)および伝導帯にある電子数
を用いて
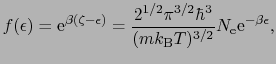 |
|
|
(5.2.15) |
と表される.ここで伝導電子の数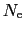 は温度の関数である.(5.2.3)-(5.2.6)式に(5.2.8)式を代入すると
は温度の関数である.(5.2.3)-(5.2.6)式に(5.2.8)式を代入すると
ここで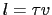 は平均自由行路であり,また伝導帯の底を
は平均自由行路であり,また伝導帯の底を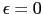 にとってある.もし
にとってある.もし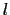 が積分に主に寄与する領域で常数
が積分に主に寄与する領域で常数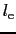 とみなせるならば,
とみなせるならば,
より
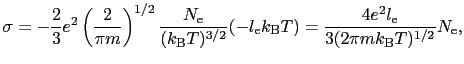 |
|
|
(5.2.17) |
が得られる.この分母はボルツマン分布した電子の平均の運動量
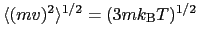 と多少の数係数の差を除いて同じものであるから,(5.2.10)式は先に求めた金属の電気伝導度の(5.2.7)式において,
と多少の数係数の差を除いて同じものであるから,(5.2.10)式は先に求めた金属の電気伝導度の(5.2.7)式において,
 ,
,
 ,
,
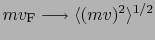 と置き換えたものと数係数の多少の違いを除いて一致している.
と置き換えたものと数係数の多少の違いを除いて一致している.




: 緩和時間
: 輸送現象
: ボルツマン方程式
目次
Masashige Onoda
平成18年4月7日
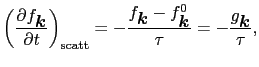
![]() による不均一がないときは,(5.1.7)と(5.2.1)式より,
による不均一がないときは,(5.1.7)と(5.2.1)式より,
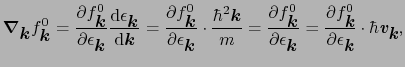
![]() は
は
![]() または
または
![]() は
は
![]() での値と理解して
での値と理解して![]() または
または![]() と表すと,(5.2.6)式は
と表すと,(5.2.6)式は
![]() は成り立たない.
は成り立たない.![]() は伝導帯の底より下にあるから,伝導帯にある電子はボルツマン分布
は伝導帯の底より下にあるから,伝導帯にある電子はボルツマン分布
![]() で与えられ,その電子数は
で与えられ,その電子数は
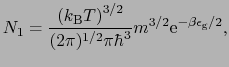
![$\displaystyle \zeta = - \frac{1}{2}\Delta\epsilon - \frac{1}{2}k_{\rm B}T{\rm l...
...ft[\frac{1}{2N_{0}\hbar^{3}}\left(\frac{2mk_{\rm B}T}{\pi}\right)^{3/2}\right],$](img639.png)