



: 不純物による散乱
: 輸送現象
: 電気伝導度
目次
(5.2.1)式で導入した緩和時間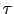 を量子力学的に考察してみよう.伝導電子が1つのブロッホ状態から他のブロッホ状態へ散乱されるのは,不純物や格子振動による格子の乱れによるのであり,その乱れは一般に自由度を含んでいる.格子振動の場合には,それはフォノンの振動数,進行方向,偏極の方向であり,不純物の場合であれば,その自由度は不純物にある電子の配置やスピンの向きである.伝導電子がこれらによって散乱されたときに,散乱体のエネルギー変化がなければ,その過程は弾性散乱であり,エネルギー変化のあるときは非弾性散乱と考えなければならない.
を量子力学的に考察してみよう.伝導電子が1つのブロッホ状態から他のブロッホ状態へ散乱されるのは,不純物や格子振動による格子の乱れによるのであり,その乱れは一般に自由度を含んでいる.格子振動の場合には,それはフォノンの振動数,進行方向,偏極の方向であり,不純物の場合であれば,その自由度は不純物にある電子の配置やスピンの向きである.伝導電子がこれらによって散乱されたときに,散乱体のエネルギー変化がなければ,その過程は弾性散乱であり,エネルギー変化のあるときは非弾性散乱と考えなければならない.
一般に摂動ポテンシャル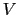 があるときに,系が
があるときに,系が
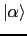 から
から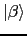 へ移る遷移確率
へ移る遷移確率
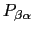 は,一次のボルン近似では
は,一次のボルン近似では
で与えられる.伝導電子の
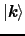 から
から
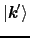 への散乱に際して散乱体のエネルギー変化を
への散乱に際して散乱体のエネルギー変化を
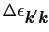 ,散乱ポテンシャルを
,散乱ポテンシャルを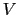 とすると上式は
とすると上式は
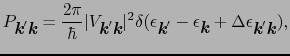 |
|
|
(5.3.18) |
となる.散乱によって単位時間に
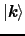 にある電子の分布の変化は,散乱でスピンは保存するとして,
にある電子の分布の変化は,散乱でスピンは保存するとして,
第1項は着目している
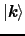 状態へ入ってくる散乱,第2項はそこから出て行く散乱を表す.
状態へ入ってくる散乱,第2項はそこから出て行く散乱を表す.
弾性散乱を考えることにして(5.3.2)式で
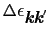 ,
,
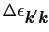 を無視しよう.
を無視しよう.
ここで(5.1.2)式を用いた.
系は等方的であるとし,
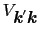 は
は
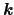 と
と
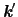 のなす角
のなす角
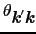 のみの関数とおく.いま仮定している緩和時間
のみの関数とおく.いま仮定している緩和時間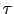 を使って
を使って
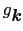 は(5.2.2)式で表されるから,
は(5.2.2)式で表されるから,
一方,(5.2.1),(5.2.2)式より,
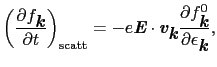 |
|
|
(5.3.21) |
であるから,(5.3.3),(5.3.4)式より
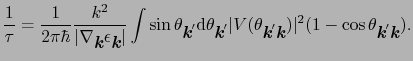 |
|
|
(5.3.22) |
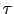 は電気伝導のような輸送現象に特有の緩和時間である.
は電気伝導のような輸送現象に特有の緩和時間である.
種々の散乱過程が存在するときには,それぞれの過程における散乱ポテンシャル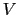 を求め,その散乱による緩和時間が上の式から得られるわけである.もしそれらが互いに独立な散乱過程であれば,それぞれの過程による緩和時間を
を求め,その散乱による緩和時間が上の式から得られるわけである.もしそれらが互いに独立な散乱過程であれば,それぞれの過程による緩和時間を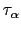 として
として
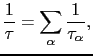 |
|
|
(5.3.23) |
で与えられる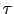 が電気抵抗を決めることになる.
が電気抵抗を決めることになる.




: 不純物による散乱
: 輸送現象
: 電気伝導度
目次
Masashige Onoda
平成18年4月7日
![]() があるときに,系が
があるときに,系が
![]() から
から![]() へ移る遷移確率
へ移る遷移確率
![]() は,一次のボルン近似では
は,一次のボルン近似では
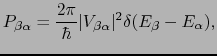
![]() ,
,
![]() を無視しよう.
を無視しよう.
![$\displaystyle \left({\partial f_{\mbox{\bfseries\itshape {k}}} \over{\partial t...
...box{\bfseries\itshape {k}}'} - \epsilon_{\mbox{\bfseries\itshape {k}}})\right].$](img668.png)
![]() は
は
![]() と
と
![]() のなす角
のなす角
![]() のみの関数とおく.いま仮定している緩和時間
のみの関数とおく.いま仮定している緩和時間![]() を使って
を使って
![]() は(5.2.2)式で表されるから,
は(5.2.2)式で表されるから,
![$\displaystyle \left({\partial f_{\mbox{\bfseries\itshape {k}}} \over{\partial t...
...pe {k}}'\mbox{\bfseries\itshape {k}}})\right]\cdot\mbox{\bfseries\itshape {E}},$](img678.png)
![]() を求め,その散乱による緩和時間が上の式から得られるわけである.もしそれらが互いに独立な散乱過程であれば,それぞれの過程による緩和時間を
を求め,その散乱による緩和時間が上の式から得られるわけである.もしそれらが互いに独立な散乱過程であれば,それぞれの過程による緩和時間を![]() として
として