



: 格子振動による散乱
: 輸送現象
: 緩和時間
目次
金属や半導体の中に価数の異なる不純物原子を入れると,母体の周期的なポテンシャル場から乱れたポテンシャルをその付近に与え,伝導電子の散乱中心として働くことになる.実際には同じ価数の不純物原子でも,その原子半径の違いや原子心におけるポテンシャルの違いから,やはり散乱中心として働くが,その効果はここでは考えないことにする.
縮退した自由電子の中に,母体の原子と価数が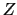 だけ異なる不純物原子を考える.その原子心の電子構造の違いは考慮しないことにしたのであるから,荷電が
だけ異なる不純物原子を考える.その原子心の電子構造の違いは考慮しないことにしたのであるから,荷電が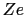 の点電荷と見なせる.
の点電荷と見なせる.
さて電子はクーロン反発力で互いに近づきにくくなるが,クーロン相互作用は長距離に働く相互作用であり,どの程度長距離にわたっての影響があるのであろうか?その問題を考えてみる.
いま一様な電荷密度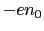 をもつ電子ガスの中に点電荷
をもつ電子ガスの中に点電荷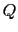 をもちこみ,その位置を原点とする.その周りの電子は影響を受けるので,
をもちこみ,その位置を原点とする.その周りの電子は影響を受けるので,
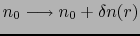 の密度の変化が起こったとする.ポアッソンの式に従って,静電的なポテンシャル
の密度の変化が起こったとする.ポアッソンの式に従って,静電的なポテンシャル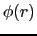 は
は
![$\displaystyle \Delta\phi(r) = -4\pi[Q\delta(\mbox{\bfseries\itshape {r}}) - e\delta n(r)],$](img687.png) |
|
|
(5.4.24) |
を満足する.電子ガスが温度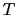 で平衡状態にあるとすると,
で平衡状態にあるとすると,
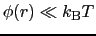 として
として
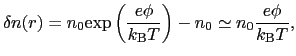 |
|
|
(5.4.25) |
と書けるから,これを(5.4.1)式に入れ,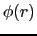 に球対称性を要請すると
に球対称性を要請すると
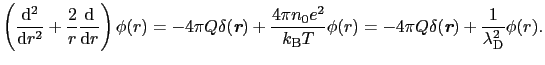 |
|
|
(5.4.26) |
ここで
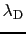 は,
は,
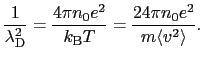 |
|
|
(5.4.27) |
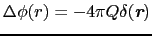 の解が
の解が
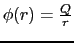 であることを用いると
であることを用いると
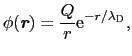 |
|
|
(5.4.28) |
であることがわかる.すなわち電荷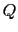 のまわりのポテンシャルは遮蔽されたクーロン型になる.その遮蔽距離
のまわりのポテンシャルは遮蔽されたクーロン型になる.その遮蔽距離
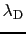 をデバイの長さとよぶ.もし放電された気体中の電子ガスとして,
をデバイの長さとよぶ.もし放電された気体中の電子ガスとして,
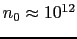 [cm
[cm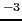 ],
],
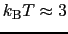 [eV]とおくと
[eV]とおくと
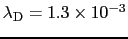 [cm]となる.金属の伝導電子を考えると,フェルミ面までの状態は電子で詰められているから,(5.4.2)式の代わりに
[cm]となる.金属の伝導電子を考えると,フェルミ面までの状態は電子で詰められているから,(5.4.2)式の代わりに
![$\displaystyle \delta n(r) = \frac{1}{3\pi^{2}}\left[\frac{2m}{\hbar^{2}}\left(\...
...\right]^{3/2} - n_{0} \simeq \frac{3}{2}\frac{n_{0}}{\epsilon_{\rm F}}e\phi(r),$](img700.png) |
|
|
(5.4.29) |
これは(5.4.2)式と同じ形で,
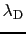 を
を
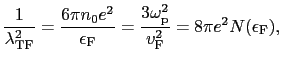 |
|
|
(5.4.30) |
で与えられる
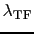 で置き換えた解を与える.
で置き換えた解を与える.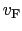 はフェルミ速度,
はフェルミ速度,
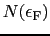 は一方のスピンあたりの
は一方のスピンあたりの
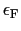 での状態密度,
での状態密度,
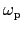 は
は
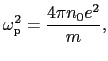 |
|
|
(5.4.31) |
で与えられるプラズマ振動数とよばれる量である.
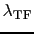 はトーマス・フェルミの遮蔽距離とよばれる.典型的な金属として,
はトーマス・フェルミの遮蔽距離とよばれる.典型的な金属として,
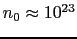 ,
,
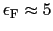 [eV]とおくと,
[eV]とおくと,
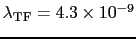 [cm]である.電子系の中では荷電体の影響を遮蔽して,クーロンポテンシャルを
[cm]である.電子系の中では荷電体の影響を遮蔽して,クーロンポテンシャルを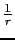 から
から
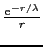 という形に変えてしまう.
という形に変えてしまう.
ボルン近似で考えると必要な量
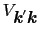 は
は
散乱ベクトルを
とおくと,弾性散乱では
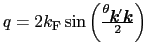 より
より
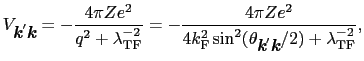 |
|
|
(5.4.33) |
となる.これを(5.3.5)式に代入して,不純物散乱による緩和時間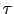 が得られる.
が得られる.
母体に単位体積当り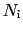 個の不純物原子があり,それらによる散乱は独立であるとすると,(5.3.6)式により
個の不純物原子があり,それらによる散乱は独立であるとすると,(5.3.6)式により
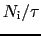 が全不純物原子からの寄与になり,そのための電気抵抗は
が全不純物原子からの寄与になり,そのための電気抵抗は
ここで(5.4.7)式より
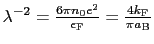 であるから,金属では
であるから,金属では
とおくことができ,(5.4.11)式の積分値は1のオーダーと考えてよい.
不純物散乱による電気抵抗の特徴は温度によらないことと,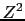 に比例することである.
に比例することである.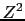 依存性をリンデの法則とよぶ.
依存性をリンデの法則とよぶ.




: 格子振動による散乱
: 輸送現象
: 緩和時間
目次
Masashige Onoda
平成18年4月7日
![]() だけ異なる不純物原子を考える.その原子心の電子構造の違いは考慮しないことにしたのであるから,荷電が
だけ異なる不純物原子を考える.その原子心の電子構造の違いは考慮しないことにしたのであるから,荷電が![]() の点電荷と見なせる.
の点電荷と見なせる.
![]() をもつ電子ガスの中に点電荷
をもつ電子ガスの中に点電荷![]() をもちこみ,その位置を原点とする.その周りの電子は影響を受けるので,
をもちこみ,その位置を原点とする.その周りの電子は影響を受けるので,
![]() の密度の変化が起こったとする.ポアッソンの式に従って,静電的なポテンシャル
の密度の変化が起こったとする.ポアッソンの式に従って,静電的なポテンシャル![]() は
は
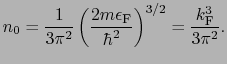
![]() は
は
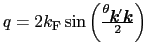 より
より
![]() 個の不純物原子があり,それらによる散乱は独立であるとすると,(5.3.6)式により
個の不純物原子があり,それらによる散乱は独立であるとすると,(5.3.6)式により
![]() が全不純物原子からの寄与になり,そのための電気抵抗は
が全不純物原子からの寄与になり,そのための電気抵抗は
![]() に比例することである.
に比例することである.![]() 依存性をリンデの法則とよぶ.
依存性をリンデの法則とよぶ.