



: 超伝導と遷移金属酸化物
: 磁性
: スピンハミルトニアン
目次
磁場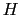
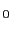 中での磁気モーメント
中での磁気モーメント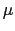 のエネルギーは,第5章で議論したように,
のエネルギーは,第5章で議論したように,
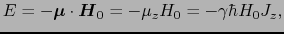 |
|
|
(6.9.86) |
である.ここで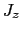 のとりうる値は,
のとりうる値は,
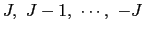 である.これをゼーマン準位と呼ぶ.隣り合う準位間のエネルギー差は,
である.これをゼーマン準位と呼ぶ.隣り合う準位間のエネルギー差は,
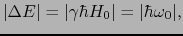 |
|
|
(6.9.87) |
となっている.これはラーモア周波数に等しい振動数のフォトン(電磁波)のエネルギーが,ちょうどゼーマン準位間のエネルギー差に等しいことを示す.そこで,このようなフォトンはレベル間の遷移を引き起こし吸収されると考えられる.これが磁気共鳴吸収の基本原理である.電子スピン共鳴(Electron Spin Resonance;略してESR)は,フォトンエネルギーとしてマイクロ波を入射し,その一部が電子系に吸収される現象である [ref9].
単位体積あたり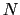 個の独立なスピン磁気モーメントがあったとき,それらのベクトル和として磁化,
個の独立なスピン磁気モーメントがあったとき,それらのベクトル和として磁化,
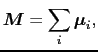 |
|
|
(6.9.88) |
が生ずる.磁場のもとで,このマクロな量であるベクトル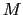 は運動方程式,
は運動方程式,
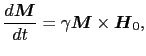 |
|
|
(6.9.89) |
に従う.既に見てきたように,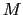 は磁場を軸とする歳差運動を行うから,
は磁場を軸とする歳差運動を行うから,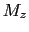 は磁場の強さに関わらず一定の値に保たれ,磁化の誘起を説明できない.磁場によって磁化が誘起されるという現象を理解するためには,スピン系のエネルギーを他へ逃がす機構を考えてやらなければならない.これをスピン-格子緩和と呼ぶ.その緩和時間を
は磁場の強さに関わらず一定の値に保たれ,磁化の誘起を説明できない.磁場によって磁化が誘起されるという現象を理解するためには,スピン系のエネルギーを他へ逃がす機構を考えてやらなければならない.これをスピン-格子緩和と呼ぶ.その緩和時間を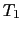 とし,
とし,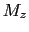 の熱平衡値を
の熱平衡値を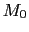 とおくと,上式にこの緩和機構を加えて,
とおくと,上式にこの緩和機構を加えて,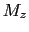 に関して,
に関して,
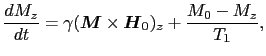 |
|
|
(6.9.90) |
という運動方程式を得る.
静磁場に対して垂直な磁化の成分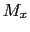 ,
,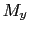 が零でないとき,これらは零に向かって減衰していく.このときスピン系のエネルギーに変化はないから,この横緩和は
が零でないとき,これらは零に向かって減衰していく.このときスピン系のエネルギーに変化はないから,この横緩和は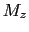 の緩和とは事情が異なる.そこで別の緩和時間を用いて,
の緩和とは事情が異なる.そこで別の緩和時間を用いて,
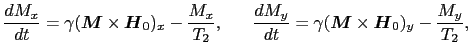 |
|
|
(6.9.91) |
という運動方程式となる.(6.9.5),(6.9.6)式はブロッホ方程式と呼ばれ,スピン磁気モーメントの振る舞いを現象論的に議論するときの出発点となる.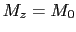 のとき,次の減衰振動の解,
のとき,次の減衰振動の解,
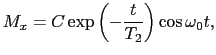 |
|
|
(6.9.92) |
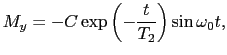 |
|
|
(6.9.93) |
を得る.
磁気共鳴の実験では,静磁場と垂直な方向に高周波磁場を加えて,その共鳴吸収を観測する.このときのスピン系の振る舞いを調べるためには,加えられた直線振動磁場
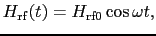 |
|
|
(6.9.94) |
を図6.10のように 面内の互いに反対方向に回る回転磁場の重ね合わせと考えると便利である.
回転磁場の大きさを
面内の互いに反対方向に回る回転磁場の重ね合わせと考えると便利である.
回転磁場の大きさを とし,角速度を
とし,角速度を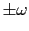 とすると,
とすると,
![$\displaystyle \mbox{\boldmath$H$}_{\rm r} = H_{1}[\mbox{\boldmath$x$}\cos\omega t + \mbox{\boldmath$y$}\sin\omega t],$](img1135.png) |
|
|
(6.9.95) |
![$\displaystyle \mbox{\boldmath$H$}_{\rm l} = H_{1}[\mbox{\boldmath$x$}\cos\omega t - \mbox{\boldmath$y$}\sin\omega t],$](img1136.png) |
|
|
(6.9.96) |
とおける.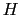
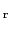 と
と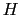
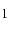 が異なるのは,
が異なるのは,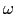 が-
が-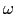 に変わる点だけである.一方の成分は磁気モーメントの歳差運動と同じ方向に回転し,他方は反対方向に回転するのであるから,共鳴の付近では反対方向の回転成分を無視してもよいだろう.そこで,
に変わる点だけである.一方の成分は磁気モーメントの歳差運動と同じ方向に回転し,他方は反対方向に回転するのであるから,共鳴の付近では反対方向の回転成分を無視してもよいだろう.そこで,
![$\displaystyle \mbox{\boldmath$H$}_{\rm 1} = H_{1}[\mbox{\boldmath$x$}\cos\omega t + \mbox{\boldmath$y$}\sin\omega t],$](img1139.png) |
|
|
(6.9.97) |
とおく.
次に,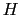
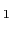 と静磁場
と静磁場
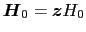 との両方の影響を含むスピンの運動方程式を求める.
との両方の影響を含むスピンの運動方程式を求める.
![$\displaystyle {d\mbox{\boldmath$\mu$} \over{dt}} = \gamma\mbox{\boldmath$\mu$}\times[\mbox{\boldmath$H$}_{0} + \mbox{\boldmath$H$}_{\rm 1}(t)],$](img1141.png) |
|
|
(6.9.98) |
において,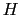
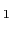 の時間依存性を除くには,
の時間依存性を除くには,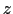 軸のまわりを振動数
軸のまわりを振動数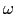 で回転する座標系に移ればよい.すなわち,そのような座標系では
で回転する座標系に移ればよい.すなわち,そのような座標系では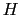
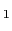 は静磁場になる.回転軸は
は静磁場になる.回転軸は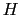
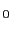 の方向と一致するから,
の方向と一致するから,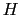
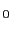 も静磁場である.そこで,回転座標系の
も静磁場である.そこで,回転座標系の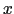 軸を
軸を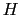
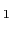 の方向にとれば,上式は,
の方向にとれば,上式は,
![$\displaystyle \left ( {d\mbox{\boldmath$\mu$} \over{dt}} \right )_{\rm r} = \mb...
...[(\omega + \gamma H_{0})\mbox{\boldmath$z$} + \gamma H_{1}\mbox{\boldmath$x$}],$](img1143.png) |
|
|
(6.9.99) |
となる.書き換えれば,
![$\displaystyle \left ( {d\mbox{\boldmath$\mu$} \over{dt}} \right )_{\rm r} = \mb...
...$x$} \right ] = \mbox{\boldmath$\mu$}\times\gamma\mbox{\boldmath$H$}_{\rm eff},$](img1144.png) |
|
|
(6.9.100) |
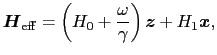 |
|
|
(6.9.101) |
となる.こうして,回転系では磁気モーメントはあたかも静磁場
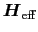 を受けているかのように振る舞うことがわかる.磁気モーメントは,
を受けているかのように振る舞うことがわかる.磁気モーメントは,
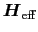 のまわりに一定の角度をなす円錐上を,角振動数
のまわりに一定の角度をなす円錐上を,角振動数
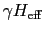 で歳差運動することになる.
で歳差運動することになる.
回転磁場が加わったときのブロッホ方程式を回転座標系で書くと,
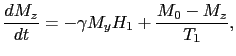 |
|
|
(6.9.102) |
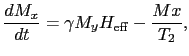 |
|
|
(6.9.103) |
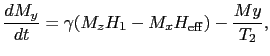 |
|
|
(6.9.104) |
となる.
図 6.11:
磁気共鳴を起こした場合の複素磁化率の角周波数依存性
|
|
上式の左側をすべて零とおいて定常解を求めると,
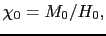 |
|
|
(6.9.107) |
を得る.直線振動磁場の振幅は2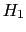 で,これと同位相の振動磁化の横成分が
で,これと同位相の振動磁化の横成分が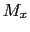 ,
,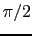 だけ遅れた成分が
だけ遅れた成分が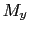 である.複素磁化率を,
である.複素磁化率を,
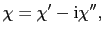 |
|
|
(6.9.108) |
とおくと,
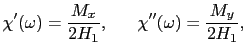 |
|
|
(6.9.109) |
である.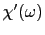 ,
,
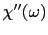 の
の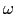 依存性を図6.11に示す.
依存性を図6.11に示す.
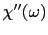 は,高周波エネルギーの吸収を表す.これは
は,高周波エネルギーの吸収を表す.これは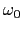 を中心としてピークを作り,その幅は
を中心としてピークを作り,その幅は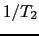 である.
である.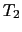 は横緩和時間,またはスピン-スピン緩和時間と呼ばれ,その逆数が共鳴吸収線の幅を与える.
は横緩和時間,またはスピン-スピン緩和時間と呼ばれ,その逆数が共鳴吸収線の幅を与える.
共鳴線の幅を与える原因としては,まず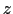 方向の磁場の分布が考えられる.各スピンが感じる磁場の強さがそのスピンの位置によって多少異なっていれば,共鳴周波数は不均一性に起因する幅をもつ.このとき,もし各スピンの感じる磁場の偏差が時間的に速くゆらいでいる場合は,歳差運動の位相のずれは平均化され,共鳴線の幅は狭くなる.これを運動による共鳴線の先鋭化と呼ぶ.このように磁気共鳴の実験は系の動的なゆらぎに関しても情報を提供できる.
方向の磁場の分布が考えられる.各スピンが感じる磁場の強さがそのスピンの位置によって多少異なっていれば,共鳴周波数は不均一性に起因する幅をもつ.このとき,もし各スピンの感じる磁場の偏差が時間的に速くゆらいでいる場合は,歳差運動の位相のずれは平均化され,共鳴線の幅は狭くなる.これを運動による共鳴線の先鋭化と呼ぶ.このように磁気共鳴の実験は系の動的なゆらぎに関しても情報を提供できる.




: 超伝導と遷移金属酸化物
: 磁性
: スピンハミルトニアン
目次
Masashige Onoda
平成18年4月7日
![]() 個の独立なスピン磁気モーメントがあったとき,それらのベクトル和として磁化,
個の独立なスピン磁気モーメントがあったとき,それらのベクトル和として磁化,
![]() ,
,![]() が零でないとき,これらは零に向かって減衰していく.このときスピン系のエネルギーに変化はないから,この横緩和は
が零でないとき,これらは零に向かって減衰していく.このときスピン系のエネルギーに変化はないから,この横緩和は![]() の緩和とは事情が異なる.そこで別の緩和時間を用いて,
の緩和とは事情が異なる.そこで別の緩和時間を用いて,
![]()
![]() と静磁場
と静磁場
![]() との両方の影響を含むスピンの運動方程式を求める.
との両方の影響を含むスピンの運動方程式を求める.
![]() 方向の磁場の分布が考えられる.各スピンが感じる磁場の強さがそのスピンの位置によって多少異なっていれば,共鳴周波数は不均一性に起因する幅をもつ.このとき,もし各スピンの感じる磁場の偏差が時間的に速くゆらいでいる場合は,歳差運動の位相のずれは平均化され,共鳴線の幅は狭くなる.これを運動による共鳴線の先鋭化と呼ぶ.このように磁気共鳴の実験は系の動的なゆらぎに関しても情報を提供できる.
方向の磁場の分布が考えられる.各スピンが感じる磁場の強さがそのスピンの位置によって多少異なっていれば,共鳴周波数は不均一性に起因する幅をもつ.このとき,もし各スピンの感じる磁場の偏差が時間的に速くゆらいでいる場合は,歳差運動の位相のずれは平均化され,共鳴線の幅は狭くなる.これを運動による共鳴線の先鋭化と呼ぶ.このように磁気共鳴の実験は系の動的なゆらぎに関しても情報を提供できる.