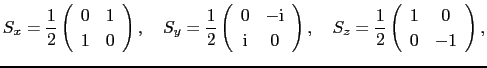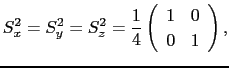: 磁気共鳴
: 磁性
: 結晶場理論
目次
結晶電場による軌道とエネルギー準位について述べたが,ここで基底状態が非縮退状態の場合のスピンに対する有効なハミルトニアンをまとめておく.
中心の磁性イオンはd電子1個のみをもち,正方晶の結晶電場に置かれた場合を考える.すなわち周りのイオンは
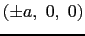 ,
,
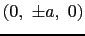 ,
,
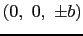 (
(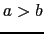 )に電荷
)に電荷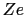 をもつ.このときエネルギー準位は
をもつ.このときエネルギー準位は
となる.ここで
である.
この種の基底状態の磁気モーメントの大きさは,この状態のエネルギーが外部磁場によっていかに変化するかを調べればよい.しかしこの外部磁場によるゼーマンエネルギーの変化に対応して,スピン-軌道結合を媒介として起こる軌道状態の変化も見落とすことはできない.したがって,ここではゼーマンエネルギーとスピン-軌道結合のエネルギーとを摂動エネルギーと考える.簡単のため,結晶場の主軸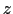 軸が常に量子化軸であるとする.摂動エネルギー
軸が常に量子化軸であるとする.摂動エネルギー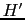 は
は
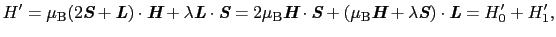 |
|
|
(6.8.76) |
となる.ところで
であるから
となる.d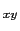 ,d
,d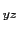 ,d
,d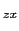 ,d
,d
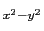 ,d
,d
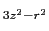 の固有関数に対しては,
の固有関数に対しては,
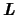 の対角要素はすべてゼロとなる.
の対角要素はすべてゼロとなる.
摂動の1次のエネルギーは基底状態について
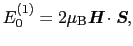 |
|
|
(6.8.77) |
となる.スピン縮重は
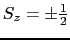 の2重であるので,各準位はこの1次摂動によって2本に分裂する.この他に,摂動エネルギーは
の2重であるので,各準位はこの1次摂動によって2本に分裂する.この他に,摂動エネルギーは
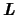 を含んでいるために各準位間の非対角成分をもっている.その影響はエネルギーの2次摂動
を含んでいるために各準位間の非対角成分をもっている.その影響はエネルギーの2次摂動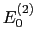 に現れる.
に現れる.
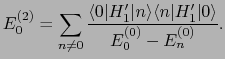 |
|
|
(6.8.78) |
上式の計算に出てくる
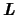 に関係した量を次のように定義しておく.
に関係した量を次のように定義しておく.
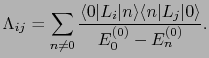 |
|
|
(6.8.79) |
そこで,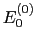 を非摂動系のエネルギーとおけば,
を非摂動系のエネルギーとおけば,
ここで
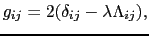 |
|
|
(6.8.80) |
とおく.前例のように,対称性の高い結晶で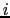 ,
,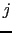 を結晶の主軸
を結晶の主軸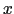 ,
,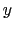 ,
,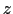 にとれるときは
にとれるときは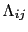 を
を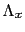 ,
,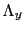 ,
,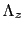 とおいて
とおいて
![$\displaystyle E_{0} = E_{0}^{(0)} + \sum_{i}\left[2(1 - \lambda\Lambda_{i})\mu_...
...- \lambda^{2}\Lambda_{i}S_{i}^{2} - \mu_{\rm B}^{2}\Lambda_{i}H_{i}^{2}\right],$](img1093.png) |
|
|
(6.8.81) |
を得る.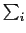 内の第1項は
内の第1項は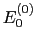 における磁気モーメントへの
における磁気モーメントへの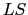 結合の影響で
結合の影響で
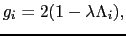 |
|
|
(6.8.82) |
は電子配置d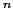 において
において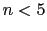 のときは
のときは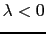 であるから
であるから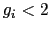 であり,
であり,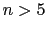 のときは
のときは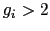 を与える.第3項は温度に依存しない帯磁率(バンブレック常磁性)を与える.
を与える.第3項は温度に依存しない帯磁率(バンブレック常磁性)を与える.
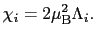 |
|
|
(6.8.83) |
第2項は磁場に関係のない項で,スピン
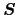 を結晶の各主軸
を結晶の各主軸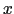 ,
,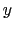 ,
,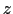 方向に向けるとき,そのエネルギーを異にする.すなわち,この項は結晶電場を起因とする結晶磁気異方性エネルギーを与え,スピンの容易軸を決定する.
方向に向けるとき,そのエネルギーを異にする.すなわち,この項は結晶電場を起因とする結晶磁気異方性エネルギーを与え,スピンの容易軸を決定する.
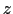 軸を球座標の軸としてスピン方向を
軸を球座標の軸としてスピン方向を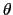 ,
,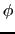 で与えると,定数項を除いて
で与えると,定数項を除いて
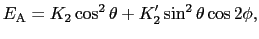 |
|
|
(6.8.85) |
と表される.
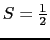 の場合,
の場合,
であるので,それらの2乗をとると
となる.すべて定数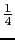 になり,
になり,
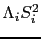 の項はスピンの向きに無関係になり,磁気異方性は生じない.この場合,
の項はスピンの向きに無関係になり,磁気異方性は生じない.この場合,
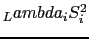 の項において正負スピンの向きの状態は縮退している.これを拡張して考えると,スピン
の項において正負スピンの向きの状態は縮退している.これを拡張して考えると,スピン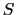 が半整数値のときは,対称の度合の低い
が半整数値のときは,対称の度合の低い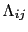 をもつ場合でも
をもつ場合でも
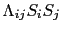 はスピン縮退を完全に取り除くことはできなくて,少なくても2重縮退が残ることが結論される.これをクラマースの定理という.
はスピン縮退を完全に取り除くことはできなくて,少なくても2重縮退が残ることが結論される.これをクラマースの定理という.




: 磁気共鳴
: 磁性
: 結晶場理論
目次
Masashige Onoda
平成18年4月7日
![]() ,
,
![]() ,
,
![]() (
(![]() )に電荷
)に電荷![]() をもつ.このときエネルギー準位は
をもつ.このときエネルギー準位は

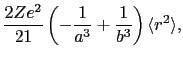
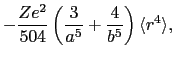
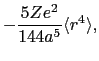
![]() 軸が常に量子化軸であるとする.摂動エネルギー
軸が常に量子化軸であるとする.摂動エネルギー![]() は
は
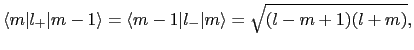
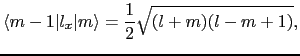
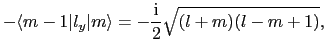
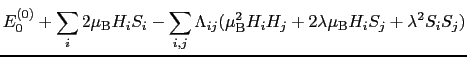
![$\displaystyle E_{0}^{(0)} + \sum_{i, j}\left[2\mu_{\rm B}H_{i}(\delta_{ij} - \l...
...ambda^{2}\Lambda_{ij}S_{i}S_{j} - \mu_{\rm B}^{2}\Lambda_{ij}H_{i}H_{j}\right].$](img1087.png)