磁束線の運動

混合状態にある第2種超伝導体では，磁束線は規則正しく並び，空間的に一様である．各磁束線の周りには超伝導電流が流れていて磁場を$\lambda$程度の距離に引き止めている．この電流は，磁束線が一様に分布していれば互いに他の磁束線による電流と打ち消しあって，全体としては電流は流れていない．

そこで外から電流を注ぎ込むとどうなるであろうか？たとえば磁場の方向を$z$軸にとり，$x$方向に電流$J$が流れているとする．$x$方向に電流ができるためには，磁束線は$y$方向に向かってだんだん濃くなっていなければならない．別の見方をすると，マクスウェル方程式より

$${\rm rot}\mbox{\bfseries\itshape {B}} = \frac{4\pi}{c}\mbox{\bfseries\itshape {J}},$$

であるから， $\mbox{\bfseries\itshape {B}} \parallel \mbox{\bfseries\itshape {z}}$， $\mbox{\bfseries\itshape {J}} \parallel \mbox{\bfseries\itshape {x}}$とすると

$$\frac{\partial B}{\partial y} = \frac{4\pi}{c}J,$$

でなければならない．磁束密度は単位面積を通過する磁束線の数を$n(y)$とすると

$$B = n(y)\varphi_{0},$$

で与えられるから，

$$\varphi_{0}\frac{{\rm d}n}{{\rm d}y} = \frac{4\pi}{c}J,$$ (7.10.74)

で，$y$方向に沿って$n$は変化していることになる．

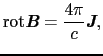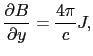磁束密度にこのような不均一があると，これを元へ戻そうとする力が働く．それは磁場のエネルギー $\frac{B^{2}}{8\pi}$をなるべく小さくするように働き，

$$\frac{\partial}{\partial y}\left(\frac{B^{2}}{8\pi}\right) = \frac{B}{4\pi}\frac{\partial B}{\partial y} = \frac{BJ}{c} = \frac{J\varphi_{0}n}{c},$$ (7.10.75)

という大きさをもつ．これは単位面積あたりの力で，$n$本の磁束線に働くと考えられるので，1本の磁束線が受ける力は

$$F = \frac{J\varphi_{0}}{c},$$ (7.10.76)

で与えられる．

一方磁束線は，半径$\xi$の部分が常伝導になっているから，金属中に常伝導になりやすい部分があると，そこにつかまってしまい，そこからなるべく離れまいとしている．金属中には不純物や転位などいろいろな格子欠陥が存在するが，この格子欠陥こそ常伝導になりやすい部分だと考えられる．つまり磁束線は，格子欠陥のある所を通り，なるべくそこに留まろうとする．いいかえると磁束線の中途で，所々がピンで止めてあると考えてよい．このピンで止めてある力を平均として$F_{\rm p}$と書くと，$F < F_{\rm p}$のうちはピンから抜けずに磁束線は動かない．しかし$F > F_{\rm p}$になると，ピンから外れて磁束線は動き出す．

磁束線が動き出すと，それは常伝導の部分からできているので，抵抗を受けると考えられる．この抵抗力が速さ$v$に比例すると考えると，磁束線の速さ$v$は

$$\eta v = F - F_{\rm p},$$ (7.10.77)

で決まることになる．

磁束線が動くと，電磁誘導の法則により電場ができる．$z$方向に向いた磁束線が$y$方向に動くから，電場は$x$方向にでき，その大きさは

$$E = \frac{v}{c}B = \frac{n\varphi_{0}}{c}v,$$ (7.10.78)

で与えられる．

(7.10.26)，(7.10.25)式を用いて，(7.10.27)式を書き直すと

$$E = \frac{B\varphi_{0}}{\eta c^{2}}J - \frac{B}{\eta c}F_{\rm p},$$ (7.10.79)

となる．ただしこの式は $\frac{\varphi_{0}}{c}J > F_{\rm p}$でのみ成り立ち，そうでないときは$E = 0$である．

(7.10.28)式は$J$の方向に電場$E$ができていることを示しており，見かけ上

$$\rho = \frac{B\varphi_{0}}{\eta c^{2}},$$ (7.10.80)

という電気抵抗を示すことを意味する．