



: 励起状態とエネルギーギャップ
: BCS理論
: BCS理論
目次
電子間の相互作用がフェルミ面付近では引力になっていると仮定する.ハミルトニアンとして,
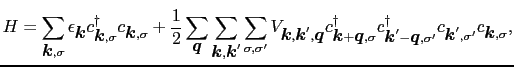 |
|
|
(7.11.81) |
をとる.
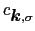 ,
,
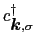 は,それぞれ運動量
は,それぞれ運動量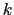 ,スピン
,スピン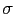 (
(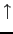 ,
,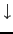 )の電子の消滅および生成演算子を表す.すなわち,
)の電子の消滅および生成演算子を表す.すなわち,
を満たす.
基底状態の波動関数として,
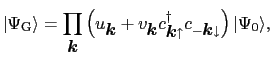 |
|
|
(7.11.82) |
をとろう.ここで
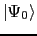 は真空状態を表す.
は真空状態を表す.
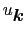 ,
,
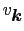 は,
は,
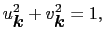 |
|
|
(7.11.83) |
の関係を満たす.(7.11.2)式では全電子数は一定でないので,その平均値がある一定値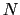 に等しいとする.すなわち,
に等しいとする.すなわち,
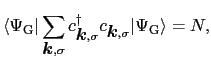 |
|
|
(7.11.84) |
とおく.
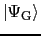 が規格化されていることは,
が規格化されていることは,
のように確かめられる.
(7.11.2)を用いて,エネルギーの期待値,
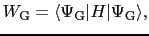 |
|
|
(7.11.86) |
を計算してみよう.
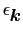 のかかる項は,(7.11.4)の条件から,
のかかる項は,(7.11.4)の条件から,
で表される.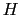 の第2項の期待値では,
の第2項の期待値では,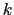 =
=
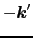 ,
,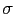 =
= 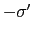 という項と,
という項と,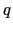 = 0,
= 0,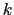
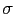 ,
,
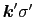 は任意という項と,
は任意という項と,
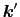 =
=
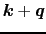 ,
,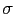 =
= 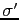 の項だけが残る.後ろの2項は,
の項だけが残る.後ろの2項は,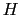 の第1項と同じ形をしているので,相互作用は小さいと仮定して無視する.こうして,
の第1項と同じ形をしているので,相互作用は小さいと仮定して無視する.こうして,
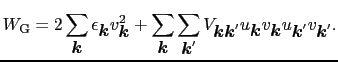 |
|
|
(7.11.87) |
(7.11.7)式を(7.11.2)式の条件下で最小にする.
であるから,
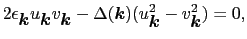 |
|
|
(7.11.88) |
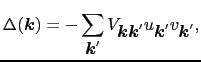 |
|
|
(7.11.89) |
を得る.(7.11.8)式と(7.11.2)式を,
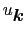 ,
,
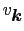 に関して解くと,
に関して解くと,
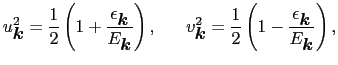 |
|
|
(7.11.90) |
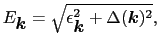 |
|
|
(7.11.91) |
となる.これらを用いて(7.11.9)式を書き直すと,
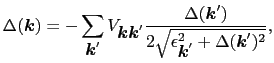 |
|
|
(7.11.92) |
となる.
次に相互作用について,
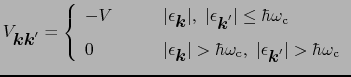 |
|
|
(7.11.93) |
の仮定をする.ここで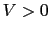 とする.(7.11.13)式を仮定すれば,(7.11.9)で与えられる
とする.(7.11.13)式を仮定すれば,(7.11.9)で与えられる
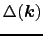 は
は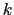 に依存しないので,
に依存しないので,
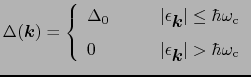 |
|
|
(7.11.94) |
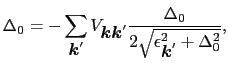 |
|
|
(7.11.95) |
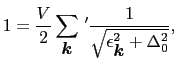 |
|
|
(7.11.96) |
となる.
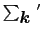 は,
は,
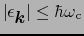 という状態についての和をとるという意味である.
という状態についての和をとるという意味である.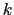 についての和を
についての和を
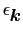 についての積分に置き換える.
についての積分に置き換える.
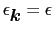 の状態密度を
の状態密度を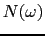 とすれば,
とすれば,
の置き換えをすればよい.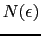 はフェルミ面
はフェルミ面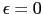 の近くでは緩やかな変化をしていると考えられるので,(7.11.16)を次式で近似する.
の近くでは緩やかな変化をしていると考えられるので,(7.11.16)を次式で近似する.
したがって,
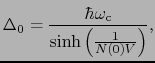 |
|
|
(7.11.97) |
を得る.
(7.11.10)式の
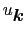 ,
,
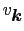 を用いて,(7.11.7)の基底状態を計算すると,
を用いて,(7.11.7)の基底状態を計算すると,
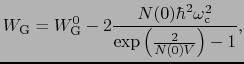 |
|
|
(7.11.98) |
となる.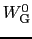 は,
は,
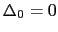 のときの(常伝導状態の)エネルギーである.
のときの(常伝導状態の)エネルギーである.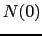
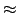 1/
1/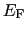 より,
より,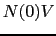
 1であるので,(7.11.17),(7.11.18)式は,
1であるので,(7.11.17),(7.11.18)式は,
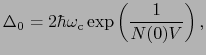 |
|
|
(7.11.99) |
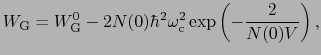 |
|
|
(7.11.100) |
のように近似される.
(7.11.10)より,
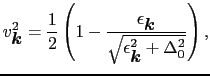 |
|
|
(7.11.101) |
である.
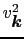 は,フェルミエネルギーより十分低い所で1,十分高い所でゼロであり,有限温度での常伝導金属のフェルミ関数に似ている.
は,フェルミエネルギーより十分低い所で1,十分高い所でゼロであり,有限温度での常伝導金属のフェルミ関数に似ている.
(7.11.19),(7.11.20)式から,
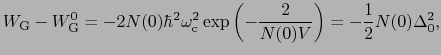 |
|
|
(7.11.102) |
となるが,これが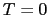 における凝縮エネルギーである.このエネルギーが
における凝縮エネルギーである.このエネルギーが
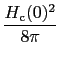 に等しくなるはずである.
に等しくなるはずである.




: 励起状態とエネルギーギャップ
: BCS理論
: BCS理論
目次
Masashige Onoda
平成18年4月7日
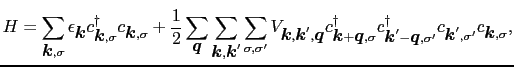
![]() のかかる項は,(7.11.4)の条件から,
のかかる項は,(7.11.4)の条件から,
![]() ,
,
![]() を用いて,(7.11.7)の基底状態を計算すると,
を用いて,(7.11.7)の基底状態を計算すると,
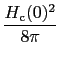 に等しくなるはずである.
に等しくなるはずである.