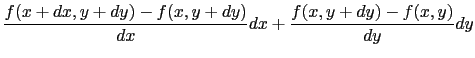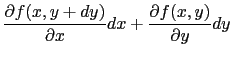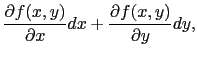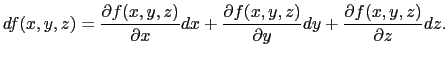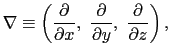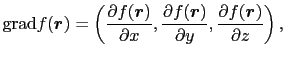: ガウスの定理
: 微分形のガウスの法則
: 微分形のガウスの法則
二個の独立変数 ,
, のうちの一個,たとえば
のうちの一個,たとえば を固定して
を固定して だけを変化させたときの関数
だけを変化させたときの関数 (
( ,
, )の変化,すなわち
)の変化,すなわち
を考えよう.これを関数 (
( ,
, )の
)の に関する偏微分係数という.また二階以上の偏微分係数,
に関する偏微分係数という.また二階以上の偏微分係数,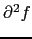 /
/
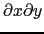 ,
,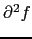 /
/
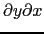 などの関数が存在し,これらの関数が連続関数であるときには,
などの関数が存在し,これらの関数が連続関数であるときには,
の関係が成り立つ.
 (
( ,
, )の全微分は
)の全微分は
で定義される.このとき,
の関係が成り立つ.このことは三変数関数 (
( ,
, ,
,  )についても同様である.
)についても同様である.
上式の偏微分の操作を形式的にベクトルの三成分とみなし,
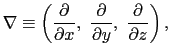 |
|
|
(1.3.38) |
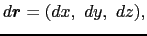 |
|
|
(1.3.39) |
とおくと,
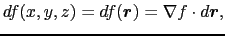 |
|
|
(1.3.40) |
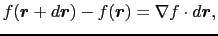 |
|
|
(1.3.41) |
となる. はナブラ(nabla)と呼ばれる.
はナブラ(nabla)と呼ばれる.
 (
( ) = 一定値
) = 一定値 とすれば,図1.10のように,これは三次元空間の中の一つの曲面
とすれば,図1.10のように,これは三次元空間の中の一つの曲面 を与える.ここで
を与える.ここで +
+ 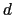
 が曲面
が曲面 上にあるときは,
上にあるときは,
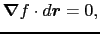 |
|
|
(1.3.42) |
となる.すなわち,

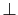
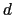
 を得る.
を得る.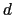
 の方向は任意にとれるので,
の方向は任意にとれるので,
 は点
は点 において面
において面 に直交するベクトルである.
に直交するベクトルである.
 は
は (
( )の勾配(グラディエント;gradient),
)の勾配(グラディエント;gradient),
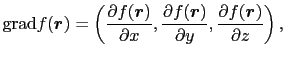 |
|
|
(1.3.43) |
を表す.



: ガウスの定理
: 微分形のガウスの法則
: 微分形のガウスの法則
Masashige Onoda
平成18年4月15日
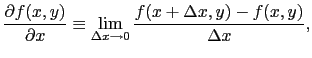
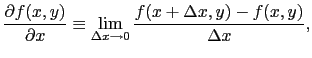
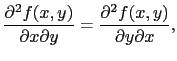
![]() (
(![]() ,
,![]() )の全微分は
)の全微分は