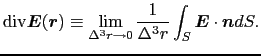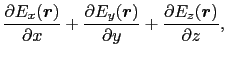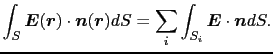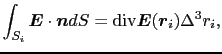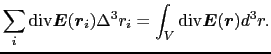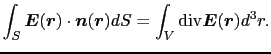: 微分形のガウスの法則
: 微分形のガウスの法則
: 偏微分法と勾配
図 1.11:
微小箱中の点電荷
|
|
図1.11のように,体積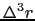
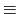
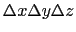 の微小な箱の中に正電荷
の微小な箱の中に正電荷 がある.
がある. の作る電場は箱の中から外向きに出ている.
の作る電場は箱の中から外向きに出ている.
この箱の表面 上で電場の面積分を行ってみよう.まず
上で電場の面積分を行ってみよう.まず 軸に関しては,
軸に関しては,
となる.上の第2式に負の符号がついたのは面Bに立てた の方向が
の方向が 軸の負の方向に相当しているからである.
軸の負の方向に相当しているからである. ,
, 軸に関しても同様の計算を行うと,最終的に,
軸に関しても同様の計算を行うと,最終的に,
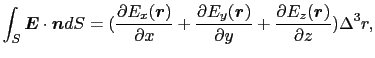 |
|
|
(1.3.44) |
が得られる.これは,体積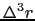
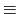
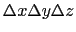 の微小な箱に対する,正電荷
の微小な箱に対する,正電荷 が作る外向き電場の正味の量に相当する.
が作る外向き電場の正味の量に相当する.
ここでdiv
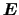 (
(
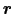 )を次式で定義しよう.divはダイバージェンス(divergence;発散)と呼ばれる.
)を次式で定義しよう.divはダイバージェンス(divergence;発散)と呼ばれる.
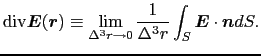 |
|
|
(1.3.45) |
式の定義から想像されるように,div (
( )は,微小な箱
)は,微小な箱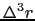 から出てくる電場の正味の量に対応している1.2.(1.3.7)式,(1.3.8)式より,
から出てくる電場の正味の量に対応している1.2.(1.3.7)式,(1.3.8)式より,
とおけることがわかる.
図 1.12:
任意の閉曲面 の内部分割
の内部分割
|
|
今度は,任意の閉曲面 曲面上で求めてみる.図1.12のように,
曲面上で求めてみる.図1.12のように, の内部を微小な箱に分割して考えればよい.このとき,互いに隣り合う箱の面上では,それぞれの面上に外向きに立てた
の内部を微小な箱に分割して考えればよい.このとき,互いに隣り合う箱の面上では,それぞれの面上に外向きに立てた の方向が反対向きになっていて,そのためにその面上の面積分は互いに相殺してしまうことに注意しよう.結局積分で残るのは,相手のない面,すなわち,全体の表面
の方向が反対向きになっていて,そのためにその面上の面積分は互いに相殺してしまうことに注意しよう.結局積分で残るのは,相手のない面,すなわち,全体の表面 からの寄与だけになる.
からの寄与だけになる.
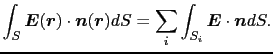 |
|
|
(1.3.48) |
(1.3.7)式より,
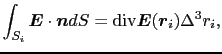 |
|
|
(1.3.49) |
であるから,
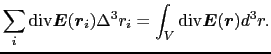 |
|
|
(1.3.50) |
となる.ここでの は,
は, によって囲まれる空間領域である.すなわち,
によって囲まれる空間領域である.すなわち,
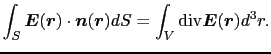 |
|
|
(1.3.51) |
この面積分を体積積分に変換する定理をガウスの定理という.この関係は, (
( )が電場であるか否かに関係なく,三個の成分をもつ任意の関数に対して常に成立する数学上の定理である.
)が電場であるか否かに関係なく,三個の成分をもつ任意の関数に対して常に成立する数学上の定理である.



: 微分形のガウスの法則
: 微分形のガウスの法則
: 偏微分法と勾配
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=1, clip]{fig-1-3-1.eps}](img213.png)
![]() 上で電場の面積分を行ってみよう.まず
上で電場の面積分を行ってみよう.まず![]() 軸に関しては,
軸に関しては,
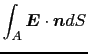
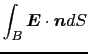
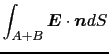
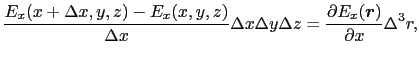
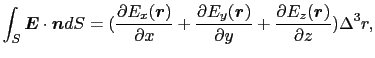
![]() (
(
![]() )を次式で定義しよう.divはダイバージェンス(divergence;発散)と呼ばれる.
)を次式で定義しよう.divはダイバージェンス(divergence;発散)と呼ばれる.