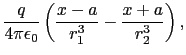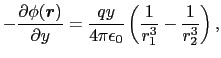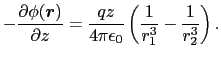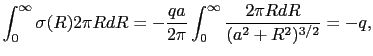: 第4回演習問題
: 静電場の基本法則とその応用例
: ポアッソン方程式の応用例
静電場の問題には,たとえば導体表面上の電位を与えて,導体外にできる静電場を決めると同時に,導体表面上の電荷分布を決めるといった種類の問題もある.この場合は,(1.4.16)式の右辺の電荷密度が未定のため,導体表面上で静電ポテンシャルが一定であるという条件のもとでラプラスの方程式を解く.これを境界値問題という.
半径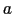 の導体球を考え,その表面上の電位が一定値
の導体球を考え,その表面上の電位が一定値
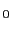 をとるものとする.
をとるものとする.
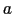 では,1.5.2節より
では,1.5.2節より
したがって
導体表面上の電荷の面密度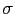 は第2回演習問題6番より,
は第2回演習問題6番より,
導体の形が複雑になると,導体表面上の境界条件を満たすラプラス方程式の解を求めることは難しくなる.しかし特別な問題の場合,微分方程式を解かなくても,境界条件を満たす解の形を予想することができる場合がある.これを鏡像法という.
図 1.19:
鏡像法:接地した平面状導体と点電荷
|
|
図1.19に示すように,接地した平面状の導体の前の点Q (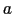 ,0,0)に点電荷
,0,0)に点電荷 をおいたとする.導体表面上の電位は0である.
をおいたとする.導体表面上の電位は0である.
導体がなければ,点電荷 による点P(
による点P( ,
, ,
, )における
)における (
( )は,
)は,
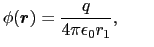 |
|
|
|
| |
|
|
(1.5.80) |
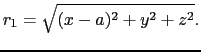 |
|
|
|
しかし,上式は導体表面上で0にならず境界条件を満たしていない.そこで導体表面を鏡の面と考えて,点電荷 の像のできる場所(-
の像のできる場所(-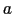 ,0,0)に点電荷-
,0,0)に点電荷- をおき,その代わりに導体をとり除いたとする.-
をおき,その代わりに導体をとり除いたとする.- が点Pに作る静電ポテンシャルは,
が点Pに作る静電ポテンシャルは,
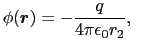 |
|
|
|
| |
|
|
(1.5.81) |
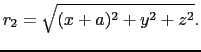 |
|
|
|
今,
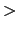 0の領域で考えている限り,上式はラプラスの方程式を満たしている.そこで,
0の領域で考えている限り,上式はラプラスの方程式を満たしている.そこで,
の和を考えよう.これは,
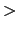 0の領域で,点電荷+
0の領域で,点電荷+ のみがあるときのポアッソン方程式を満たし,また導体表面上で0になり,要求されている境界条件を満足している.こうして,
のみがあるときのポアッソン方程式を満たし,また導体表面上で0になり,要求されている境界条件を満足している.こうして,
したがって導体表面上( = 0)の電場は,
= 0)の電場は,
導体表面に誘導されている電荷の面密度は,
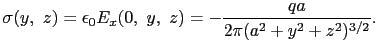 |
|
|
(1.5.82) |
全誘導電荷の量は,上式を導体表面の全体にわたって積分することによって得られる.導体上の原点Oを中心とする極座標系をとれば,
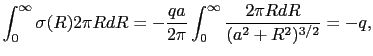 |
|
|
(1.5.83) |
となる.すなわち全誘導電荷量は点電荷 の電荷量に等しく,その符号は反対である.このような静電誘導を完全誘導という.
の電荷量に等しく,その符号は反対である.このような静電誘導を完全誘導という.



: 第4回演習問題
: 静電場の基本法則とその応用例
: ポアッソン方程式の応用例
Masashige Onoda
平成18年4月15日
![]() の導体球を考え,その表面上の電位が一定値
の導体球を考え,その表面上の電位が一定値![]()
![]() をとるものとする.
をとるものとする.![]()
![]()
![]() では,1.5.2節より
では,1.5.2節より
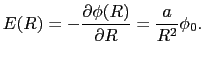
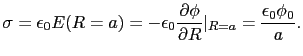
![]() による点P(
による点P(![]() ,
,![]() ,
,![]() )における
)における![]() (
(![]() )は,
)は,
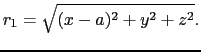
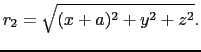
![$\displaystyle \phi(\mbox{\boldmath$r$})
=
{q\over{4\pi\epsilon_{0}}} \left [ {1...
...{2} + y^{2} + z^{2}}}} - {1\over{\sqrt{(x + a)^{2} + y^{2} + z^{2}}}} \right ],$](img359.png)
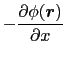
![$\displaystyle {q\over{4\pi\epsilon_{0}}} \left \{ {x - a\over{\left [ (x - a)^{...
... - {x + a\over{ \left [ (x + a)^{2} + y^{2} + z^{2} \right ]^{3/2}}} \right \},$](img362.png)