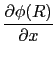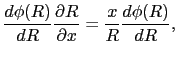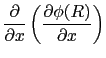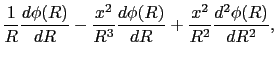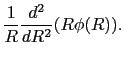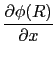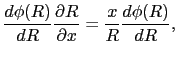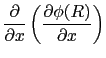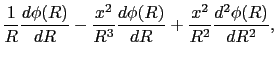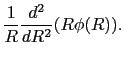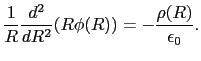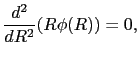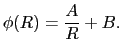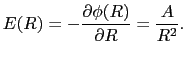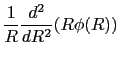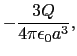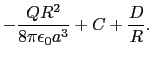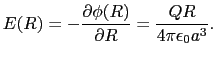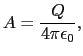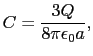: 境界値問題,鏡像法
: 静電場の基本法則とその応用例
: 静電場の基本法則
ポアッソン方程式から出発して,半径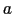 の球内に全電荷
の球内に全電荷 が一様に分布しているときの電場を求めてみよう.(第2回演習問題3番,第3回演習問題2番を参照のこと)静電ポテンシャルは球の中心Oからの距離
が一様に分布しているときの電場を求めてみよう.(第2回演習問題3番,第3回演習問題2番を参照のこと)静電ポテンシャルは球の中心Oからの距離 だけの関数
だけの関数 (
( )で表されるはずである.座標原点を球の中心O中心に選ぶと,
)で表されるはずである.座標原点を球の中心O中心に選ぶと,
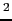 =
= 
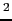 +
+ 
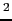 +
+ 
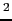 であるので,
であるので,
したがって,ポアッソン方程式は次の微分方程式に帰着する.

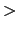
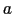 では
では (
( ) = 0より,
) = 0より,
ここで
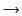
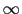 で
で (
( )
) 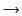 0とすれば,
0とすれば, = 0.したがって,
= 0.したがって,

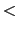
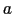 では,
では,
 = 0で
= 0で (0)は有限であるから
(0)は有限であるから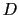 = 0でなければならない.したがって,
= 0でなければならない.したがって,
また球面( =
= 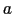 )における連続の条件から
)における連続の条件から
が得られる.



: 境界値問題,鏡像法
: 静電場の基本法則とその応用例
: 静電場の基本法則
Masashige Onoda
平成18年4月15日