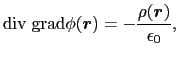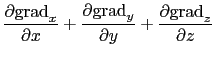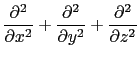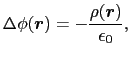静電場の基本法則

これまでの節で導出された重要な法則は，

$${\rm div}\mbox{\boldmath$E$}(\mbox{\boldmath$r$}) = {\rho(\mbox{\boldmath$r$})\over{\epsilon_{0}}}$$ (1.5.73)

$${\rm rot}\ \mbox{\boldmath$E$}(\mbox{\boldmath$r$}) = 0,$$ (1.5.74)

の二つである．(1.5.2)式の条件から，$\phi$( )，

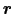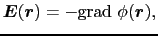$$\mbox{\boldmath$E$}(\mbox{\boldmath$r$}) = - {\rm grad} \ \phi(\mbox{\boldmath$r$}),$$ (1.5.75)

が導かれる．(1.5.3)式を(1.5.1)式に代入すると，

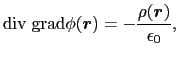$${\rm div \; grad} \phi(\mbox{\boldmath$r$}) = -{\rho(\mbox{\boldmath$r$})\over{\epsilon_{0}}},$$ (1.5.76)

が得られる．ここでdiv gradの演算子は次のように書き換えられる．

$${\rm div \; grad} = {\partial {\rm grad}_{x}\over{\partial x}} + {\partial {\rm grad}_{y}\over{\partial y}} + {\partial {\rm grad}_{z}\over{\partial z}}$$

$$= {\partial^{2}\over{\partial x^{2}}} + {\partial^{2}\over{\partial y^{2}}} + {\partial^{2}\over{\partial z^{2}}}$$ (1.5.77)

$$\equiv \Delta.$$

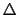上式の$\Delta$をラプラシアン（Laplacian）という．これを用いれば(1.5.4)式は，

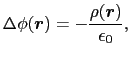$$\Delta \phi(\mbox{\boldmath$r$}) = -{\rho(\mbox{\boldmath$r$})\over{\epsilon_{0}}},$$ (1.5.78)

となる．これをポアッソン（Poisson）の方程式という．特に，右辺の電荷密度の値が0，

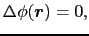$$\Delta \phi(\mbox{\boldmath$r$}) = 0,$$ (1.5.79)

である場合，ラプラス（Laplace）の方程式ともいう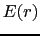．$E(r)$を求めるには，(1.5.6)式あるいは(1.5.7)式の偏微分方程式を解いた後で(1.5.3)式を用いればよい．

以下では，ポアッソン方程式の応用などについて考えよう^1.3．