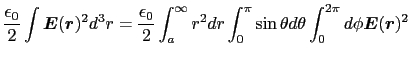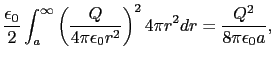: コンデンサーとその静電容量
: 静電場のエネルギー
: 静電場のエネルギー
図 1.20:
電荷 を受けとった半径
を受けとった半径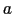 の導体球
の導体球
|
|
図1.20のように,半径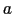 の導体球に電荷
の導体球に電荷 を与えたとする.このとき,まわりの空間における静電ポテンシャルは,導体球の中心から観測点までの距離を
を与えたとする.このとき,まわりの空間における静電ポテンシャルは,導体球の中心から観測点までの距離を とすると,
とすると,
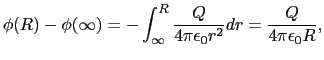 |
|
|
(1.6.84) |
となる.ここで (
(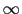 )は,
)は,
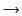
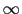 での電位である.導体球面上の電位は,
での電位である.導体球面上の電位は,
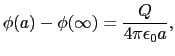 |
|
|
(1.6.85) |
となる.ここで電位差 (
(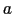 ) -
) -  (
(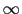 )の値を1 [V]だけ上昇させるに要する導体球上の電荷の増加量を
)の値を1 [V]だけ上昇させるに要する導体球上の電荷の増加量を とすると,
とすると,
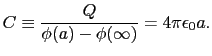 |
|
|
(1.6.86) |
一般に空間内に孤立して置かれた導体において,それに与えた電荷 とその表面
とその表面 上の電位
上の電位 (
( )と無限の遠方の電位
)と無限の遠方の電位 (
(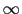 )の電位差の比,
)の電位差の比,
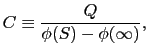 |
|
|
(1.6.87) |
を孤立導体の静電容量という.
図 1.21:
微小電荷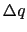 の移動
の移動
|
|
電荷 が導体表面上に分布しているとき,これにさらに微小電荷
が導体表面上に分布しているとき,これにさらに微小電荷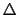
 を無限の遠方からもってきて,導体表面
を無限の遠方からもってきて,導体表面 上まで運び込む(図1.21).このとき外からなすべき仕事の量
上まで運び込む(図1.21).このとき外からなすべき仕事の量
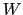 は,
は,
![$\displaystyle \Delta W
=
\Delta q \int_{\infty}^{\rm A}{\rm grad} \phi(\mbox{\boldmath$r$}) \cdot d\mbox{\boldmath$r$}
=
\Delta q [\phi(S) - \phi(\infty)],$](img380.png) |
|
|
(1.6.88) |
である.Aは導体表面上の任意の点である.
 を導体に近づけると,一般には導体表面上の電荷の分布は変化し,それに伴って電荷
を導体に近づけると,一般には導体表面上の電荷の分布は変化し,それに伴って電荷 の作る静電ポテンシャルも変化するが,ここではそのような変化を無視できるほど,
の作る静電ポテンシャルも変化するが,ここではそのような変化を無視できるほど,
 は微小な電荷であるとする.ここで(1.6.4)式を用いると,
は微小な電荷であるとする.ここで(1.6.4)式を用いると,
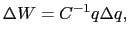 |
|
|
(1.6.89) |
と書ける.すなわち,はじめ帯電していない導体に次々に電荷を運び込み,最後に導体上の電荷が になるまでに外からなす仕事の全量は,
になるまでに外からなす仕事の全量は,
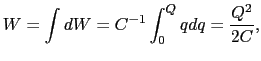 |
|
|
(1.6.90) |
で表される.これが導体のもつ静電エネルギー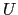
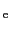 である.上式では,
である.上式では,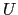
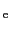 は導体そのものに蓄えられているという表現になっている.
は導体そのものに蓄えられているという表現になっている.
ファラデーは,このエネルギーが空間内に生じたエーテルの歪みのエネルギーとして,空間内に蓄えられていると考えた. (
(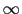 ) = 0とすると,静電エネルギーは,
) = 0とすると,静電エネルギーは,
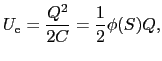 |
|
|
(1.6.91) |
と書ける.導体表面を微小面に分割し, 上の点Aにおける微小面の面積を
上の点Aにおける微小面の面積を
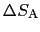 ,その場所の電荷の表面密度を
,その場所の電荷の表面密度を
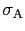 と書くと,
と書くと,
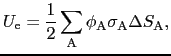 |
|
|
(1.6.92) |
と表される.ここで
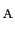 は点Aの電位で,これは導体表面の全体で同じ値をもつ.
は点Aの電位で,これは導体表面の全体で同じ値をもつ.
図1.22のように,導体外の空間内の静電場の等電位面を,
とし,それらの間の微小間隔を,
とおく.また,
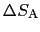 ,
, 
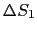 ,
, 
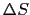
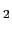 ,
, 
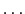 面上の電場の大きさを,
とおくと,ガウスの法則から
面上の電場の大きさを,
とおくと,ガウスの法則から
と書ける.したがって,
と表される.ここで
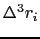
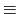
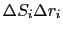 とした.こうして,
とした.こうして,
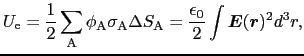 |
|
|
(1.6.93) |
となる.(1.6.10)式で表された静電エネルギーは(1.6.8)式と異なり,空間内に蓄えられているということは明らかである.空間内の場所 におけるエネルギー密度は,
におけるエネルギー密度は,
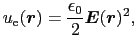 |
|
|
(1.6.94) |
となる.
(1.6.10)式を用いれば,半径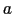 の導体球に電荷
の導体球に電荷 を与えたときの静電場のエネルギーは,
を与えたときの静電場のエネルギーは,
となる.



: コンデンサーとその静電容量
: 静電場のエネルギー
: 静電場のエネルギー
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=0.9, clip]{fig-1-6-1.eps}](img374.png)
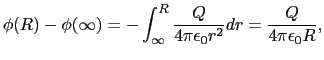
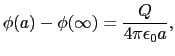
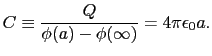
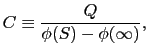
![$\displaystyle \Delta W
=
\Delta q \int_{\infty}^{\rm A}{\rm grad} \phi(\mbox{\boldmath$r$}) \cdot d\mbox{\boldmath$r$}
=
\Delta q [\phi(S) - \phi(\infty)],$](img380.png)
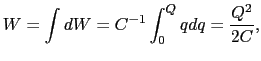
![]() (
(![]() ) = 0とすると,静電エネルギーは,
) = 0とすると,静電エネルギーは,
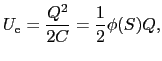
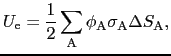
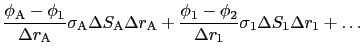
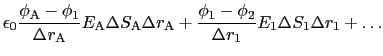
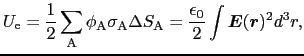
![]() の導体球に電荷
の導体球に電荷![]() を与えたときの静電場のエネルギーは,
を与えたときの静電場のエネルギーは,