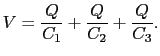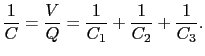: 第5回演習問題
: 静電場のエネルギー
: 静電場のエネルギー
2個の導体を考え,それらに正負の等量の電荷を与えるとき,正に帯電した導体Aから出た電気力線がすべて負に帯電した導体Bで終わるような体系をコンデンサーという.コンデンサーの静電容量は,これらの導体間の電位差 (A)-
(A)- (B)を1 [V]上昇させるのに要する電荷量
(B)を1 [V]上昇させるのに要する電荷量 をもって定義される.すなわち,
をもって定義される.すなわち,
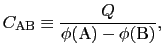 |
|
|
(1.6.95) |
で表される.コンデンサーの電位差を1 [V]上昇させるのに要する電荷量が1 [C]であるとき,その静電容量を1 [F](ファラッド)とし,これを静電容量の単位とする.すなわち,
1 [F] = 1 [C/V] = 1 [A
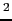
s
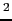
N
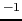
m
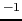
],
面積 の長方形の導体板を距離
の長方形の導体板を距離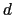 をおいて平行に並べたときの静電容量を求めてみよう.2枚の導体板をそれぞれ+
をおいて平行に並べたときの静電容量を求めてみよう.2枚の導体板をそれぞれ+ ,-
,- に帯電させる.極板の大きさに比べて極板間の距離が十分小さいときは端の影響は無視できて,電荷は極板の表面上に一様に分布する.いま正に帯電した導体の表面にまたがる微小円筒を考えて,ガウスの法則を用いると,電場は,
に帯電させる.極板の大きさに比べて極板間の距離が十分小さいときは端の影響は無視できて,電荷は極板の表面上に一様に分布する.いま正に帯電した導体の表面にまたがる微小円筒を考えて,ガウスの法則を用いると,電場は,
で与えられる.したがって静電ポテンシャルは,
と書ける.ここで は定数,
は定数, は正に帯電した極板からの距離である.こうして,
は正に帯電した極板からの距離である.こうして,
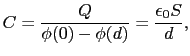 |
|
|
(1.6.96) |
が得られる.
図 1.23:
コンデンサーの接続;(a) 並列,(b) 直列
|
|
コンデンサーは電荷を蓄える容器である.しかし個々のコンデンサーの容量には制限があり,またそれらの耐電圧にも限りがある.そこで,いくつかのコンデンサーを接続して,目的に応じたコンデンサーをつくる必要が生じてくる.図1.23(a)のように並列接続の場合は,コンデンサーにかかる電圧はみな等しい.すなわち,
全体の電荷量は =
= 
 +
+ 
 +
+ 
 であるので,合成容量は,
であるので,合成容量は,
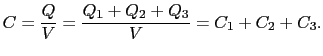 |
|
|
(1.6.97) |
並列のときの合成容量は各容量の和に等しく,静電容量を大きくできる.
次に図1.23(b)のような直列接続について考えよう.接続前には各コンデンサーに電荷はないとし,図の一番左側のコンデンサーの正極に+ を与える.
を与える.
また全電位差は =
= 
 +
+ 
 +
+ 
 であるので,
であるので,
合成容量は,
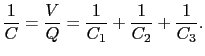 |
|
|
(1.6.98) |
 は,
は,
 ,
,
 ,
,
 のどれよりも小さくなる.直列にしたときの
のどれよりも小さくなる.直列にしたときの は小さくなるが,それぞれのコンデンサーにかかる電圧は小さくなる.全体としての耐電圧を大きくできる.
は小さくなるが,それぞれのコンデンサーにかかる電圧は小さくなる.全体としての耐電圧を大きくできる.



: 第5回演習問題
: 静電場のエネルギー
: 静電場のエネルギー
Masashige Onoda
平成18年4月15日
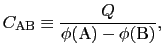
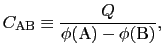
![]() の長方形の導体板を距離
の長方形の導体板を距離![]() をおいて平行に並べたときの静電容量を求めてみよう.2枚の導体板をそれぞれ+
をおいて平行に並べたときの静電容量を求めてみよう.2枚の導体板をそれぞれ+![]() ,-
,-![]() に帯電させる.極板の大きさに比べて極板間の距離が十分小さいときは端の影響は無視できて,電荷は極板の表面上に一様に分布する.いま正に帯電した導体の表面にまたがる微小円筒を考えて,ガウスの法則を用いると,電場は,
に帯電させる.極板の大きさに比べて極板間の距離が十分小さいときは端の影響は無視できて,電荷は極板の表面上に一様に分布する.いま正に帯電した導体の表面にまたがる微小円筒を考えて,ガウスの法則を用いると,電場は,
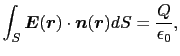
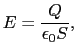
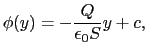
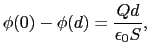
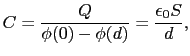
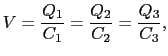
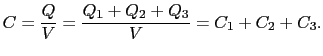
![]() を与える.
を与える.