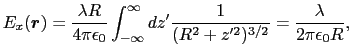: 第1回演習問題
: 静電場
: 静電場
ガラス棒を絹糸でこすったり,樹脂棒を毛皮でこすってみると,これらの棒は紙片などをよく引きつける.これらの棒は,目には見えないが,何かを帯びたと考えられる.この何かを,電気または電荷と呼び,電気を帯びることを帯電するという.
図 1.1:
(a) 電気振り子と (b) クーロンのねじり秤
|
|
図1.1(a)のような電気振り子を用いると,電気の基本的な性質を調べることができる.これは,軽いコルク球を絹糸でガラスの支柱につるしたもので,以下の現象をとらえることができる.
- 絹でこすったガラス棒をコルク球に近づけると,コルク球は棒に引きつけられる.
- ガラス棒にコルク球が接触した瞬間にコルク球は勢いよく反発する.
- 毛皮でこすった樹脂棒の場合も,上記と同じ現象を起こす.
- ガラス棒に触れて帯電したコルク球に,帯電した樹脂棒を近づけるとコルク球は引きつけられる.
- ガラス棒に触れて帯電したコルク球と毛皮でこすった樹脂棒が接触すると電気的性質がなくなる.
1の現象は静電誘導と呼ばれる現象である.すなわち,ガラス棒の帯びた電荷を正と定義すれば,ガラス棒側に面したコルク球面には負の電荷が発生したために,引力が働いたのである.2の現象は,ガラス棒上の電荷の一部がコルク球に移り,それらの電荷間に斥力が働いたためである.3,4,5の現象は,樹脂棒の帯びた電荷を負と定義すれば,すべて説明されることがわかるだろう.
電気を帯びた物体が何個かあるとき,これらの物体の大きさが相互の距離に比べて小さいならば,これらを大きさのない帯電体(点電荷)として扱うことができる.点電荷という考えは,問題を扱う上での一つの理想化(近似)である.クーロンは1785年に図1.1(b)のような装置をつくり,点電荷間に作用する力の大きさ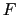 を,糸のねじれと釣り合わせることにより測定した結果,次の法則が成立することを見出した.
を,糸のねじれと釣り合わせることにより測定した結果,次の法則が成立することを見出した.
それぞれ電荷 と
と をもつ二個の点電荷の間の距離を
をもつ二個の点電荷の間の距離を ,それらの間に作用する力の大きさを
,それらの間に作用する力の大きさを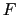 と書くと
と書くと
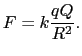 |
|
|
(1.1.1) |
ここで,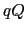
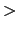 0のとき斥力,
0のとき斥力,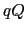
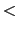 0のとき引力が作用する.これをクーロンの法則という.
0のとき引力が作用する.これをクーロンの法則という.
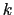 の値は電荷の単位を決めることによって決定される.本講義では次のMKSA単位系を用いることにする.
の値は電荷の単位を決めることによって決定される.本講義では次のMKSA単位系を用いることにする.
長さ = [m],質量 = [kg],時間 = [s],電流の単位 = [A],電荷の単位 = 1 [A
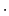
s] = 1 [C].
1 [N] = 1 [kg m s
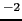
],1 [J] = 1 [kg m
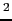
s
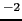
] = 1 [N m].
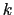 が決定される:
が決定される:

=

= 1 [C],

= 1 [m]のとき,
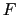
= 8.9876
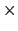
10
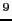
[N].
これから,
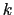 の代わりに,真空の誘電率
の代わりに,真空の誘電率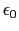 を用いて,
を用いて,
とおけば,
![$\displaystyle \epsilon_{0} = {1\over{4 \pi k}} = 8.854 \times 10^{-12} [{\rm A^{2} s^{2} N^{-1} m^{-2}}].$](img50.png) |
|
|
(1.1.2) |
4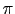 を引き出しておくのは,こうすることにより後に現れる基本法則に単位半径の球の表面積4
を引き出しておくのは,こうすることにより後に現れる基本法則に単位半径の球の表面積4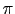 が出てこないからである(有理単位系).
が出てこないからである(有理単位系).
こうしてMKSA有理単位系で,クーロンの法則は次のように表される.
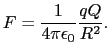 |
|
|
(1.1.3) |
(1.1.3)式を万有引力の法則で与えられる重力と比較してみよう.二個の質点の質量をそれぞれ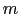 [kg],
[kg],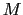 [kg],その間の距離を
[kg],その間の距離を [m]としたとき,質点間に働く力の大きさ
[m]としたとき,質点間に働く力の大きさ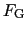 [N]は,
[N]は,
となる.今,二個の質点として電子を考えると,電子の質量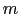 =
= 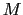 = 9.1
= 9.1 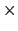 10
10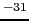 [kg],電荷量
[kg],電荷量 =
=  = -1.6
= -1.6 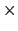 10
10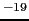 [C]を用いて,クーロン力と重力の比は,
[C]を用いて,クーロン力と重力の比は,
となる.クーロン力は重力に比べて圧倒的に大きいことがわかる.このために原子や分子の世界では,重力の効果は無視され,クーロン力が有効な力となる.地球上の物体に重力が作用するのは,原子や分子のほとんどすべてが電気的に中性であって,電気的作用が相殺してしまうからである.
次に,クーロンの法則をベクトル形式で表現しよう.
図1.2のように,原点Oから点電荷 および点電荷
および点電荷 の位置に引いた位置ベクトルを,それぞれ
の位置に引いた位置ベクトルを,それぞれ
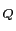 ,
,
 ,何もない空間の場所を
,何もない空間の場所を とおくと,
とおくと,
となるので,点電荷 が点電荷
が点電荷 に作用する力は,
に作用する力は,
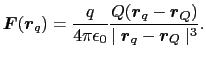 |
|
|
(1.1.4) |
 個の点電荷
個の点電荷
 ,
,
 ,
,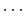 ,
,
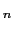 がそれぞれ
がそれぞれ
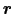
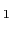 ,
,
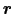
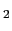 ,
,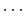 ,
,
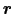
 の位置にあるとき,これらが点電荷
の位置にあるとき,これらが点電荷 に作用する力は
に作用する力は
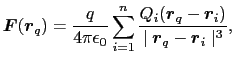 |
|
|
(1.1.5) |
となる.これは実験事実に基づくもので,「重ね合わせの原理」という.
クーロンの法則は「遠隔作用」の考え方に慣れていた時代に発見されたので,ニュートンの力学体系に新しい力を一つ加えたものにすぎないものとして理解された.しかしファラデー(1791〜1867)には,二個の電荷の間に作用する力が遠隔作用によるものであるとは考えられなかった.帯電体のまわりの空間には目に見えないゴムの棒のようなものがのびていて,そのゴム棒を通して電荷間に力が作用すると考えた.ゴム棒のなかの歪みが,その中を次々と伝わって電荷間に力が作用する,という考え方を「近接作用」の考え方という.
クーロンの法則を次のように二つの式に分解する.
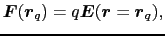 |
|
|
(1.1.6) |
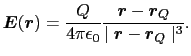 |
|
|
(1.1.7) |
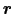 = (
= ( ,
, ,
, )は空間内の任意の場所を指定する座標値,
)は空間内の任意の場所を指定する座標値,
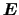 (
(
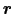 )は位置
)は位置
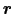
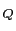 にある点電荷
にある点電荷 が任意の場所
が任意の場所
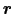 に作る歪みの大きさと方向,すなわち電場を表す.時間的に変化しない電場を静電場という.
に作る歪みの大きさと方向,すなわち電場を表す.時間的に変化しない電場を静電場という.
多数の点電荷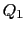 ,
,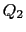 ,
, ,
,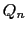 がある場合は,
がある場合は,
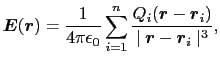 |
|
|
(1.1.8) |
となる.
電荷が連続的に分布しているときの電場を考えよう.図1.3に示すように,空間を微小な領域に分割し,その微小領域の場所に番号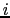 を付けて
を付けて
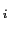 でその場所を指定する.このとき全電荷量
でその場所を指定する.このとき全電荷量
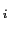 は,電荷密度を
は,電荷密度を (
(
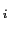 )とおくと,
)とおくと,
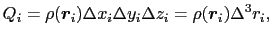 |
|
|
(1.1.9) |
とおけるので,
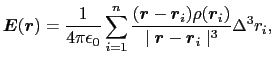 |
|
|
(1.1.10) |
を得る.ここで
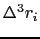 を無限小にしたとき,上式の和の値が微小領域の分割の仕方によらずに一定値に収束する場合は,
を無限小にしたとき,上式の和の値が微小領域の分割の仕方によらずに一定値に収束する場合は,
となる.複数の積分はまだ習っていないかもしれないが,要は, ,
, ,
,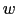 に関する積分をそれぞれ忠実に行えばよい.
に関する積分をそれぞれ忠実に行えばよい.
上の積分表式と点電荷系における表式との関係を調べる.点電荷に対する電荷密度を表す便利な方法として,次のデルタ関数を用いる方法がある.
| |
|
|
(1.1.12) |
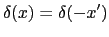 |
|
|
|
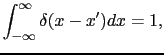 |
|
|
(1.1.13) |
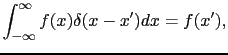 |
|
|
(1.1.14) |
三次元的なデルタ関数は次式で与えられる.
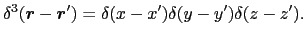 |
|
|
(1.1.15) |
位置
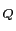 にある点電荷
にある点電荷 の場所
の場所 における電荷密度は,
における電荷密度は,
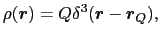 |
|
|
(1.1.16) |
 個の点電荷が分布しているときの電荷密度は,
個の点電荷が分布しているときの電荷密度は,
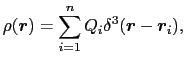 |
|
|
(1.1.17) |
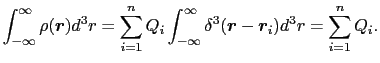 |
|
|
(1.1.18) |
図 1.4:
無限に長い一様な直線状の電荷の作る静電場
|
|
単位長さ当りの電荷量を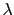 とする,無限に長い一様な直線状の電荷の作る静電場を二通りの方法で求めてみよう.
とする,無限に長い一様な直線状の電荷の作る静電場を二通りの方法で求めてみよう.
図1.4の針金の微小部分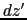 の電荷
の電荷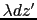 は,点電荷とみなすことができる.この電荷は点P = (
は,点電荷とみなすことができる.この電荷は点P = ( , 0, 0)に次の電場を作る.
, 0, 0)に次の電場を作る.
対称性から,針金全体の作る電場に寄与するのは,針金に直交する方向の成分である.すなわち,
次に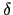 関数を用いて解いてみよう.針金の太さを無視すれば,針金上の電荷密度は,
関数を用いて解いてみよう.針金の太さを無視すれば,針金上の電荷密度は,
これを(1.1.11)式に代入すると,観測点 = (
= ( ,
,  ,
,  )における電場の
)における電場の 成分は,
成分は,
同様にして,
観測点Pでは, =
=  ,
, =
=  = 0より,
= 0より,



: 第1回演習問題
: 静電場
: 静電場
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=0.8, clip]{fig-1-1-1.eps}](img36.png)
![]() を,糸のねじれと釣り合わせることにより測定した結果,次の法則が成立することを見出した.
を,糸のねじれと釣り合わせることにより測定した結果,次の法則が成立することを見出した.
![]() と
と![]() をもつ二個の点電荷の間の距離を
をもつ二個の点電荷の間の距離を![]() ,それらの間に作用する力の大きさを
,それらの間に作用する力の大きさを![]() と書くと
と書くと
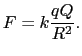
![]() の値は電荷の単位を決めることによって決定される.本講義では次のMKSA単位系を用いることにする.
の値は電荷の単位を決めることによって決定される.本講義では次のMKSA単位系を用いることにする.
![$\displaystyle k = {FR^{2}\over{qQ}} = 8.9876 \times 10^{9} [{\rm N m^{2} A^{-2} s^{-2}}].$](img47.png)
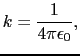
![$\displaystyle \epsilon_{0} = {1\over{4 \pi k}} = 8.854 \times 10^{-12} [{\rm A^{2} s^{2} N^{-1} m^{-2}}].$](img50.png)
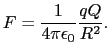
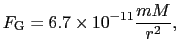
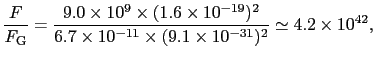
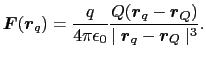
![]() 個の点電荷
個の点電荷![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]() がそれぞれ
がそれぞれ
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() の位置にあるとき,これらが点電荷
の位置にあるとき,これらが点電荷![]() に作用する力は
に作用する力は
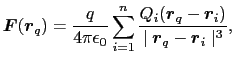
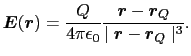
![]() ,
,![]() ,
,![]() ,
,![]() がある場合は,
がある場合は,
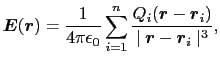
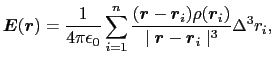
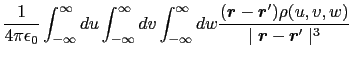
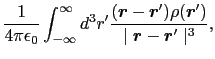
![\begin{displaymath}\delta (x - x') = \left\{
\begin{array}{ll}
\displaystyle{\in...
... [0.2cm]
\displaystyle{0}&
\qquad x \ne x'
\end{array} \right. \end{displaymath}](img88.png)
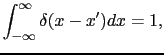
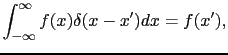
![]()
![]() にある点電荷
にある点電荷![]() の場所
の場所![]() における電荷密度は,
における電荷密度は,
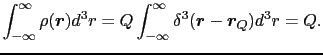
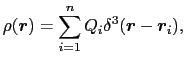
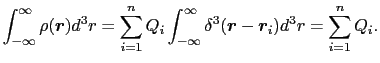
![]() の電荷
の電荷![]() は,点電荷とみなすことができる.この電荷は点P = (
は,点電荷とみなすことができる.この電荷は点P = (![]() , 0, 0)に次の電場を作る.
, 0, 0)に次の電場を作る.
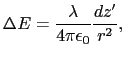
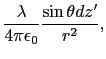
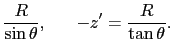
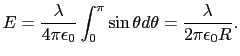
![]() 関数を用いて解いてみよう.針金の太さを無視すれば,針金上の電荷密度は,
関数を用いて解いてみよう.針金の太さを無視すれば,針金上の電荷密度は,
![$\displaystyle E_{x}(\mbox{\boldmath$r$}) = {\lambda \over{4\pi\epsilon_{0}}} \i...
...}} \int_{-\infty}^{\infty} dz' {1 \over{[x^{2} + y^{2} + (z - z')^{2}]^{3/2}}}.$](img109.png)
![$\displaystyle {\lambda y \over{4\pi\epsilon_{0}}} \int_{-\infty}^{\infty} dz' {1 \over{[x^{2} + y^{2} + (z - z')^{2}]^{3/2}}},$](img111.png)
![$\displaystyle {\lambda \over{4\pi\epsilon_{0}}} \int_{-\infty}^{\infty} dz' {z - z' \over{[x^{2} + y^{2} + (z - z')^{2}]^{3/2}}}.$](img113.png)