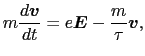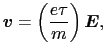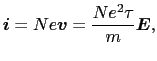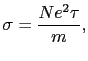: ジュールの法則
: オームの法則
: オームの法則
図2.2に示すように,導線上の二点間の電位差を
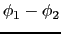 (
(
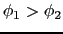 )としたとき,その二点間に流れる電流の強さ
)としたとき,その二点間に流れる電流の強さ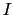 は電位差に比例する.この比例定数を
は電位差に比例する.この比例定数を とおけば,
とおけば,
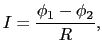 |
|
|
(2.2.5) |
と与えられる.これを「オームの法則」という. を電気抵抗といい,それは実験によると導線の二点間の長さ
を電気抵抗といい,それは実験によると導線の二点間の長さ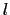 に比例し,その断面積
に比例し,その断面積 に反比例する.すなわち,
に反比例する.すなわち,
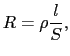 |
|
|
(2.2.6) |
と表される. を抵抗率とよび,導線の形や長さに関係しない.
を抵抗率とよび,導線の形や長さに関係しない. の逆数
の逆数
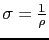 を電気伝導度という.電気抵抗の単位は,1 [
を電気伝導度という.電気抵抗の単位は,1 [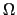 (オーム)] = 1 [VA
(オーム)] = 1 [VA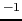 ]で表される.
]で表される.
(2.2.1)の法則を近接作用の立場に適合した形式に書き直そう.
図2.3のような断面積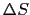 ,長さ
,長さ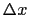 の微小な円筒を考え,その全電気抵抗を
の微小な円筒を考え,その全電気抵抗を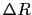 とおく.円筒の底面の電位を
とおく.円筒の底面の電位を
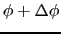 ,上面の電位を
,上面の電位を とすると,円筒導体内の電流
とすると,円筒導体内の電流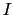 は下から上へ流れる.すなわち電位の上昇方向と,電流の方向は反対向きであるから,
は下から上へ流れる.すなわち電位の上昇方向と,電流の方向は反対向きであるから,
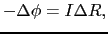 |
|
|
(2.2.7) |
となる.電流密度を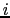 とすると,
とすると,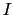 =
= 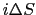 ,また(2.2.2)より,
,また(2.2.2)より,
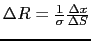 であるので,
であるので,
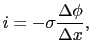 |
|
|
(2.2.8) |
と表される.これをベクトル形式で書き直すと,
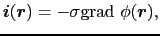 |
|
|
(2.2.9) |
となる.導体内に電位差のある場合も,電場は,
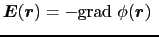 |
|
|
(2.2.10) |
と表されるので,
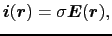 |
|
|
(2.2.11) |
となる.
静電的現象においては,帯電した導体の電荷は常にその表面上に分布している.その意味で,電荷の流れが電流であるならば,その電流は導体の表面上を流れるのではないか?と考えてしまうかもしれない.しかし,このときは電気抵抗が導線の半径に反比例するはずで,「電気抵抗は導線の断面積に反比例し,電流は導体の内部を流れている」という実験結果と一致しない.
導体内の電子の運動の様子を調べることによって,オームの法則を導こう.電子の質量を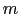 ,電荷を
,電荷を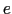 とすると,電子の運動方程式は,
とすると,電子の運動方程式は,
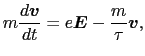 |
|
|
(2.2.12) |
で与えられる. は導体内の電場,第2項は導体を構成する原子との衝突を表し,
は導体内の電場,第2項は導体を構成する原子との衝突を表し,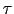 は緩和時間である.加速力と減速力が釣り合ったとき,電子の運動は定常的になる.このとき,
は緩和時間である.加速力と減速力が釣り合ったとき,電子の運動は定常的になる.このとき,
が成立する.導体の単位体積中の自由電子数を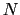 とおくと,単位時間当り,単位面積の断面を通過する電荷量は
とおくと,単位時間当り,単位面積の断面を通過する電荷量は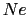
 で与えられるので,電流密度は,
で与えられるので,電流密度は,
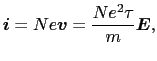 |
|
|
(2.2.13) |
となる.(2.2.7)式と(2.2.9)式より
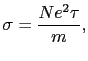 |
|
|
(2.2.14) |
を得る.



: ジュールの法則
: オームの法則
: オームの法則
Masashige Onoda
平成18年4月15日
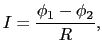
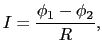
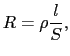
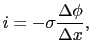
![]() ,電荷を
,電荷を![]() とすると,電子の運動方程式は,
とすると,電子の運動方程式は,