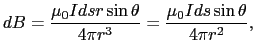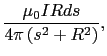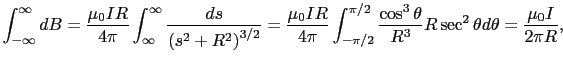: 第9回演習問題
: 電流と磁場
: 第8回演習問題
これまでは磁場の中の定常電流に作用する力の法則を調べてきたが,今度は,定常電流のつくる磁場を決定する法則を考える.
図 3.5:
直線状の針金に流された定常電流の作る磁場
|
|
エルステッドの発見を知ったビオとサバールとは,直線状の針金に定常電流を流し,絹糸につるした小磁針をそのそばにおき,その振動の周期を測定した(図3.5).これにより,定常電流のまわりに生じた磁場の強さを測定した.その結果,定常電流のまわりの磁束密度の強さ が電流の強さ
が電流の強さ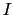 に比例し,針金からの距離
に比例し,針金からの距離 に反比例すること,すなわち,
に反比例すること,すなわち,
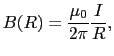 |
|
|
(3.4.10) |
を見出した.ここで
 [N A
[N A ]である.
]である.
図3.6のように磁場の方向を考慮して
 は,
は,
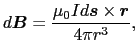 |
|
|
(3.4.11) |
と表すことができる.これをビオとサバールの法則という.ここで電荷素片は実在しうるが,電流素片というものは実在しないことに注意しなければならない.本当に物理的意味をもつのは(3.4.2)式ではなくて,定常電流の閉曲線 の全体にわたって線積分を行ったものである.すなわち,
の全体にわたって線積分を行ったものである.すなわち,
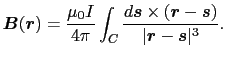 |
|
|
(3.4.12) |
である.
(3.4.2)式を用いて,無限に長い,強さ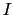 の直線電流が,直線から
の直線電流が,直線から だけ離れた点Pにつくる磁場を求めてみる.図3.7のように点Pから直線に下ろした垂線の足Oを原点とし,原点から距離
だけ離れた点Pにつくる磁場を求めてみる.図3.7のように点Pから直線に下ろした垂線の足Oを原点とし,原点から距離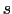 にある微小部分
にある微小部分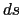 部分のつくる磁場
部分のつくる磁場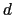
 を考える.
を考える.
図 3.7:
直線電流が,直線から だけ離れた点Pにつくる磁場
だけ離れた点Pにつくる磁場
|
|
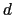
 は
は
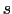 と
と の両方に垂直だから,図の紙面に垂直で手前から向こう側に向かっている.このとき,(3.4.2)式において
の両方に垂直だから,図の紙面に垂直で手前から向こう側に向かっている.このとき,(3.4.2)式において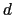
 の方向は
の方向は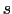 によらないことになるので,
によらないことになるので,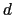
 の大きさだけを加え合わせればよい.大きさは,
の大きさだけを加え合わせればよい.大きさは,
である.ここで,
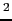 =
= 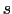
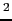 +
+ 
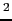 ,sin
,sin 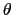 =
= 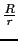 を用いると,
を用いると,
となる.



: 第9回演習問題
: 電流と磁場
: 第8回演習問題
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=1, clip]{fig-3-4-1.eps}](img563.png)
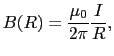
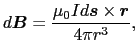
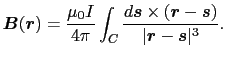
![]() の直線電流が,直線から
の直線電流が,直線から![]() だけ離れた点Pにつくる磁場を求めてみる.図3.7のように点Pから直線に下ろした垂線の足Oを原点とし,原点から距離
だけ離れた点Pにつくる磁場を求めてみる.図3.7のように点Pから直線に下ろした垂線の足Oを原点とし,原点から距離![]() にある微小部分
にある微小部分![]() 部分のつくる磁場
部分のつくる磁場![]()
![]() を考える.
を考える.