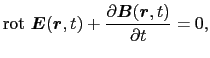: 運動する導線内に発生する起電力
: 電磁誘導
: 電磁誘導
「電流が磁気的現象を示す.」というエルステッドの発見後,ファラデーは「磁気的現象に基づいて電流を発生させることができるはずである.」と考えて研究をはじめた.そして,1831年8月29日,電磁誘導現象を発見することに成功した.これは,ある針金を流れる電流の電磁効果によって,他の針金中に電気を引き起こすもので,現代の電気技術の基礎となっている.ファラデーの誘導リング(図4.1)は最初の変圧器である.
ファラデーは,直径6インチ,厚さ1インチ以下の軟鉄製のリングに針金を二重に巻きつけた.ここで,針金の各層間および針金−針金間は絶縁させた.ファラデーはリングと針金の巻き方を述べた後,次のように記した.
- コイルAの両端を電池に接続した.ただちに磁針にはっきりとした効果が認められた.磁針は振動し,最後にははじめの位置に止まった.
- コイルAと電池を切り離した.磁針のゆれが再び生じた.(まず上と反対の向きに動いてから)
- ボール紙製の筒の上にコイルを二重に巻いても同じ効果を示すことができたが,効果の強さは鉄製芯の場合の方が断然優れていた.
コイルAに電流が流れはじめるとコイルBに効果が生じる.これは電流磁気による電気の誘導であり,電磁誘導と呼ばれる.上の発見をきっかけにして,ファラデーは次の場合に電流を発生させることができることを示した.
- 一方のコイルの電流の強さを変化させたとき.
- 一方のコイルに一定の強さの電流を流しておき,他方のコイルの位置を移動したとき.
- 一つのコイルを磁石のそばにおき,その磁石を動かしたとき.
これらの実験結果をまとめると,コイルに発生する起電力 は,コイルによって囲まれた面上での磁束密度の面積分,すなわち,「コイルを切る磁束
は,コイルによって囲まれた面上での磁束密度の面積分,すなわち,「コイルを切る磁束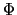 」の時間的変化の割合に比例する.この起電力によってコイル内に発生する電流の方向は磁束の変化を妨げる方向である.
」の時間的変化の割合に比例する.この起電力によってコイル内に発生する電流の方向は磁束の変化を妨げる方向である.
図 4.2:
コイル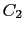 における磁束
における磁束
|
|
式で示せば,
となる.
(4.1.1)式では,図4.2のようなコイル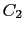 内の起電力の原因を,コイル
内の起電力の原因を,コイル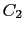 に囲まれた曲面
に囲まれた曲面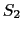 上の磁束の変化に求めているので,これは遠隔作用的な表現である.近接作用の立場で考えてみよう.
上の磁束の変化に求めているので,これは遠隔作用的な表現である.近接作用の立場で考えてみよう.
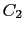 内に発生する起電力を,コイル内にできた電場
内に発生する起電力を,コイル内にできた電場 に起因するものとして,
に起因するものとして,
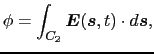 |
|
|
(4.1.3) |
と表す.ここで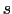 は
は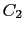 上の1点の位置を表し,線積分の方向は上図の正の方向にとるものとする.
上の1点の位置を表し,線積分の方向は上図の正の方向にとるものとする.
(4.1.2)式の磁束は一義的に決まる量であることを示しておく.磁場に関するガウスの法則,
を,上図
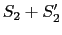 の閉曲面(体積
の閉曲面(体積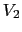 )に適用すると,
)に適用すると,
となる.したがって,
である.(4.1.2)式と(4.1.3)式を(4.1.1)式に代入すると,
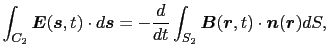 |
|
|
(4.1.4) |
である.上式で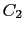 はコイル上にあり,
はコイル上にあり, (
(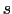 ,
,  )はそのコイル内に発生する電場であることに注意しよう.
)はそのコイル内に発生する電場であることに注意しよう.
さてファラデーはここで重大な飛躍をする.実験が直接示しているのは,コイルの内部に起電力,つまり電場が発生するということであって,コイルを離れた空間内に電場が発生するということではない.しかし,ファラデーは導線回路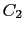 の存否にかかわらず,磁束の変化に伴って空間内に電場が生じると考えた.そして,たまたまその電場内にコイル
の存否にかかわらず,磁束の変化に伴って空間内に電場が生じると考えた.そして,たまたまその電場内にコイル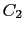 がおかれると,そのコイル内の点電荷
がおかれると,そのコイル内の点電荷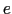 に
に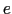
 なる力が作用して,コイル内に電流が発生すると考えた.
なる力が作用して,コイル内に電流が発生すると考えた.
上の考えに立つと,(4.1.4)式は,
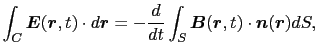 |
|
|
(4.1.5) |
となる. は,空間内に任意に想定した閉曲線であって,コイルが存在するとは考えていない.右辺の曲面
は,空間内に任意に想定した閉曲線であって,コイルが存在するとは考えていない.右辺の曲面 は,このように想定した閉曲線
は,このように想定した閉曲線 によって囲まれた任意の曲面である.この想定した閉曲線
によって囲まれた任意の曲面である.この想定した閉曲線 と曲面
と曲面 とを固定しておいたとき,(4.1.5)式の右辺は,
とを固定しておいたとき,(4.1.5)式の右辺は,
となる.(4.1.5)式の左辺は,ストークスの定理により,
となる.したがって(4.1.5)式は,
![$\displaystyle \int_{S} \left [ {\rm rot}\ \mbox{\boldmath$E$}(\mbox{\boldmath$r...
...ver{\partial t}} \right ] \cdot \mbox{\boldmath$n$}(\mbox{\boldmath$r$})dS
=
0,$](img656.png) |
|
|
(4.1.6) |
と表される.ここで曲面 を任意の点
を任意の点 上の微小面
上の微小面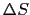 面にとると,
面にとると,
であり, (
( )の方向は任意にとれるので,
)の方向は任意にとれるので,
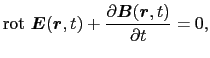 |
|
|
(4.1.7) |
を得る.上式が場所 における磁束密度
における磁束密度 (
( ,
,  )の時間的変化に伴って,その場所に発生する電場
)の時間的変化に伴って,その場所に発生する電場 (
( ,
,  )を与える法則であり,微分形におけるファラデーの誘導法則という.
)を与える法則であり,微分形におけるファラデーの誘導法則という.



: 運動する導線内に発生する起電力
: 電磁誘導
: 電磁誘導
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=1, clip]{fig-4-1-1.eps}](img638.png)
![]() は,コイルによって囲まれた面上での磁束密度の面積分,すなわち,「コイルを切る磁束
は,コイルによって囲まれた面上での磁束密度の面積分,すなわち,「コイルを切る磁束![]() 」の時間的変化の割合に比例する.この起電力によってコイル内に発生する電流の方向は磁束の変化を妨げる方向である.
」の時間的変化の割合に比例する.この起電力によってコイル内に発生する電流の方向は磁束の変化を妨げる方向である.
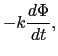
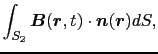
![]() 内の起電力の原因を,コイル
内の起電力の原因を,コイル![]() に囲まれた曲面
に囲まれた曲面![]() 上の磁束の変化に求めているので,これは遠隔作用的な表現である.近接作用の立場で考えてみよう.
上の磁束の変化に求めているので,これは遠隔作用的な表現である.近接作用の立場で考えてみよう.
![]() 内に発生する起電力を,コイル内にできた電場
内に発生する起電力を,コイル内にできた電場![]() に起因するものとして,
に起因するものとして,
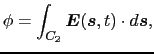
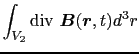
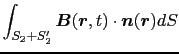
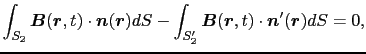
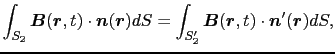
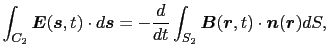
![]() の存否にかかわらず,磁束の変化に伴って空間内に電場が生じると考えた.そして,たまたまその電場内にコイル
の存否にかかわらず,磁束の変化に伴って空間内に電場が生じると考えた.そして,たまたまその電場内にコイル![]() がおかれると,そのコイル内の点電荷
がおかれると,そのコイル内の点電荷![]() に
に![]()
![]() なる力が作用して,コイル内に電流が発生すると考えた.
なる力が作用して,コイル内に電流が発生すると考えた.
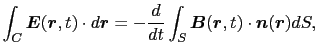
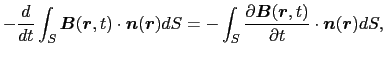
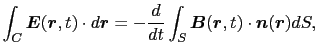
![$\displaystyle \int_{S} \left [ {\rm rot}\ \mbox{\boldmath$E$}(\mbox{\boldmath$r...
...ver{\partial t}} \right ] \cdot \mbox{\boldmath$n$}(\mbox{\boldmath$r$})dS
=
0,$](img656.png)
![$\displaystyle \left [ {\rm rot}\ \mbox{\boldmath$E$}(\mbox{\boldmath$r$}, t) + ...
...rtial t}} \right ] \cdot \mbox{\boldmath$n$}(\mbox{\boldmath$r$}) \Delta S
=
0,$](img657.png)