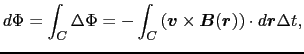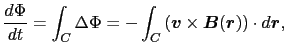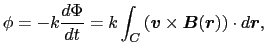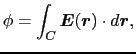: 第11回演習問題
: 電磁誘導
: 電磁誘導の法則
(4.1.1)式の法則は,(4.1.7)式の場合のように (
( ,
,  )の時間的変化によって誘導電場
)の時間的変化によって誘導電場 (
( ,
,  )が発生することのほかに,時間的に一定な磁場の中で導線回路を運動させたとき,その回路を切る磁束が変化し,それに伴ってその回路内に起電力が発生することも表している.
)が発生することのほかに,時間的に一定な磁場の中で導線回路を運動させたとき,その回路を切る磁束が変化し,それに伴ってその回路内に起電力が発生することも表している.
いま,磁束密度は時間的に変化せず (
( )で表されるとしよう.この磁場の中でコイル
)で表されるとしよう.この磁場の中でコイル を速度
を速度 で動かす.微小時間
で動かす.微小時間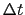 の間におけるコイルの移動距離と方向とは
の間におけるコイルの移動距離と方向とは
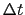 で与えられる.この移動したコイルを
で与えられる.この移動したコイルを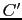 で表す.このとき次の関係が成り立つ.
で表す.このとき次の関係が成り立つ.
「コイル
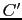
を貫く磁束
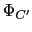
」
= 「

を貫く磁束
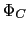
」 + 「

と
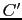
とでつくられる立体の側面を貫く磁束
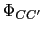
」
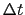 の間における磁束の変化
の間における磁束の変化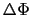 は,
は, と
と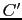 とでつくられる立体の側面を貫く磁束によって与えられる.
とでつくられる立体の側面を貫く磁束によって与えられる.
したがって,側面全体を貫く磁束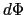 は,
は,
となる.単位時間当りの磁束の変化は,
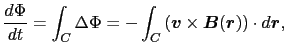 |
|
|
(4.2.9) |
となる.(4.2.2)式を(4.1.1)式に代入することにより,コイル内に発生する起電力 は,
は,
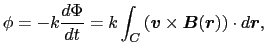 |
|
|
(4.2.10) |
と書ける.一方(4.1.3)式から,
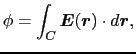 |
|
|
(4.2.11) |
であるので,(4.2.3)式と(4.2.4)式を組み合わせることにより,
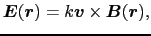 |
|
|
(4.2.12) |
を得る.(4.2.5)式で与えられる誘導電場 の存在する導線内の1点
の存在する導線内の1点
 に点電荷
に点電荷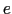 があると,これに働く力は,
があると,これに働く力は,
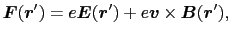 |
|
|
(4.2.13) |
となる.(4.2.6)式はローレンツ力にほかならない.これから(4.1.1)式の比例定数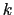 は1でなければならないことがわかる.
は1でなければならないことがわかる.



: 第11回演習問題
: 電磁誘導
: 電磁誘導の法則
Masashige Onoda
平成18年4月15日
![]() (
(![]() )で表されるとしよう.この磁場の中でコイル
)で表されるとしよう.この磁場の中でコイル![]() を速度
を速度![]() で動かす.微小時間
で動かす.微小時間![]() の間におけるコイルの移動距離と方向とは
の間におけるコイルの移動距離と方向とは![]()
![]() で与えられる.この移動したコイルを
で与えられる.この移動したコイルを![]() で表す.このとき次の関係が成り立つ.
で表す.このとき次の関係が成り立つ.