


: 磁性体中の静磁場
: マクスウェルの方程式と電磁波
: マクスウェルの方程式と電磁波
電荷の総量はいかなる物理的変化の過程においても一定不変である.いま図5.1に示されているような空間的領域 を考えると,その領域を囲む閉曲面
を考えると,その領域を囲む閉曲面 を通って単位時間に流出する正味の電荷の総量は,
を通って単位時間に流出する正味の電荷の総量は,
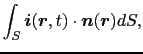 |
|
|
(5.1.1) |
図 5.1:
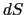 を通って単位時間に流出する電荷量
を通って単位時間に流出する電荷量
|
|
となる.ここで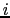 (
( ,
,  )は点
)は点 から閉曲面
から閉曲面 を通って流出する電流密度であり,
を通って流出する電流密度であり, (
( )は閉曲面
)は閉曲面 上の点
上の点 に外向きに立てた単位法線ベクトルである.電荷の総量が不変であることから,(5.1.1)式は領域
に外向きに立てた単位法線ベクトルである.電荷の総量が不変であることから,(5.1.1)式は領域 内に存在した電荷量の単位時間当りの減少量
内に存在した電荷量の単位時間当りの減少量
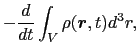 |
|
|
(5.1.2) |
に等しくなければならない. (
( ,
,  )は電荷密度を表している.したがって,電荷保存則は次のように表される.
)は電荷密度を表している.したがって,電荷保存則は次のように表される.
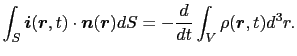 |
|
|
(5.1.3) |
(5.1.3)式を微分形で表そう.
より,
となる.したがって任意の場所で,
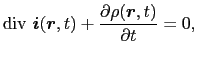 |
|
|
(5.1.4) |
の関係が成立する.
第2章で述べた定常電流においては,任意の領域 から流出する正味の電荷の量は0であり,領域
から流出する正味の電荷の量は0であり,領域 内の電荷量は変化しない.このときには,
内の電荷量は変化しない.このときには,
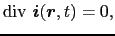 |
|
|
(5.1.5) |
となる.これが定常電流の保存則である.
Masashige Onoda
平成18年4月15日
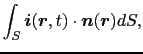
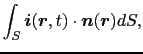
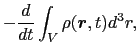
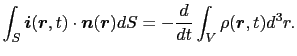
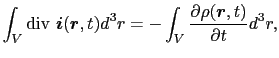
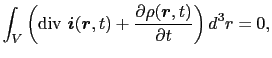
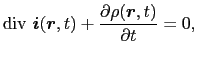
![]() から流出する正味の電荷の量は0であり,領域
から流出する正味の電荷の量は0であり,領域![]() 内の電荷量は変化しない.このときには,
内の電荷量は変化しない.このときには,