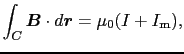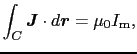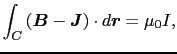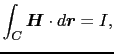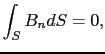: 変位電流
: マクスウェルの方程式と電磁波
: 電荷保存則
図5.2のように,ドーナッツ形の鉄にコイルを巻いて電流を流すと,コイルの内部を中空にしておいたときと比較して,そのなかに生じる磁束密度は著しく増大する.
アンペールは,上の現象を次のように解釈した.ソレノイド内の鉄を構成している鉄の分子は微小な円形電流であって,普通の状態の鉄はその中心軸が勝手な方向を向いている微小円形電流(分子電流という)の集合体であると考える.(現代物理学では,電子の自転,すなわちスピンが強い磁性の原因であることがわかっているが5.1,ここでは古典物理学的に議論を進めよう.)ソレノイドに電流を流さないときには,鉄の内部の分子電流の巨視的な平均値は0になっている.これに対し電流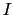 を流すと,ソレノイドの内部には一定方向の磁場ができ,この磁場が勝手な方向を向いていた分子電流の中心軸の方向を,磁場の方向に揃える.揃えられた分子電流の方向は,外から与えた電流と同じ方向を向いている.鉄の分子の分布密度が一様であるときには,鉄の内部の隣りどうしの分子電流は互いに消しあって,巨視的には鉄の表面上の分子電流だけが働き,その巨視的平均値が磁化電流
を流すと,ソレノイドの内部には一定方向の磁場ができ,この磁場が勝手な方向を向いていた分子電流の中心軸の方向を,磁場の方向に揃える.揃えられた分子電流の方向は,外から与えた電流と同じ方向を向いている.鉄の分子の分布密度が一様であるときには,鉄の内部の隣りどうしの分子電流は互いに消しあって,巨視的には鉄の表面上の分子電流だけが働き,その巨視的平均値が磁化電流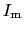 として鉄の表面上に現れる.この磁化電流のつくる磁場が,ソレノイドの電流のつくる磁場と重ね合わさって,磁束密度が増大するというのがアンペールの考えである.物体に磁化電流が生じるとき,これを磁化といい,このように磁化を起こす物質を狭義の磁性体という5.2.
として鉄の表面上に現れる.この磁化電流のつくる磁場が,ソレノイドの電流のつくる磁場と重ね合わさって,磁束密度が増大するというのがアンペールの考えである.物体に磁化電流が生じるとき,これを磁化といい,このように磁化を起こす物質を狭義の磁性体という5.2.
アンペールの法則の積分形は,
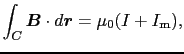 |
|
|
(5.2.6) |
と書ける.ここで磁化電流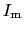 のつくる磁場を
のつくる磁場を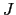 と書き,これを磁化ベクトルと呼ぼう.
と書き,これを磁化ベクトルと呼ぼう.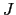 は
は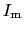 のつくる磁場であるから,
のつくる磁場であるから,
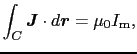 |
|
|
(5.2.7) |
となる.(5.2.2)式を(5.2.1)式に代入すると,
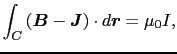 |
|
|
(5.2.8) |
となる.ここで, -
- 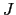 =
= 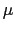
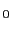
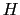 として磁場の強さ
として磁場の強さ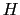 という量を導入すると,
という量を導入すると,
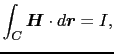 |
|
|
(5.2.9) |
の関係を得る.
(5.2.3),(5.2.4)式を微分形で表せば,それぞれ,
![$\displaystyle {\rm rot}\ \left [ \mbox{\boldmath$B$}(\mbox{\boldmath$r$}) - \mb...
...mbox{\boldmath$r$}) \right ]
=
\mu_{0}\mbox{\boldmath$i$}(\mbox{\boldmath$r$}),$](img693.png) |
|
|
(5.2.10) |
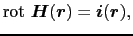 |
|
|
(5.2.11) |
で与えられる.
一方,磁場に関するガウスの法則
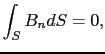 |
|
|
(5.2.12) |
は,磁性体中でも磁束密度 の磁束線は常に閉曲線をつくっているので,そのまま成立する.微分形で表せば,
の磁束線は常に閉曲線をつくっているので,そのまま成立する.微分形で表せば,
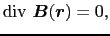 |
|
|
(5.2.13) |
である.



: 変位電流
: マクスウェルの方程式と電磁波
: 電荷保存則
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=1, clip]{fig-5-3-1.eps}](img685.png)
![]() を流すと,ソレノイドの内部には一定方向の磁場ができ,この磁場が勝手な方向を向いていた分子電流の中心軸の方向を,磁場の方向に揃える.揃えられた分子電流の方向は,外から与えた電流と同じ方向を向いている.鉄の分子の分布密度が一様であるときには,鉄の内部の隣りどうしの分子電流は互いに消しあって,巨視的には鉄の表面上の分子電流だけが働き,その巨視的平均値が磁化電流
を流すと,ソレノイドの内部には一定方向の磁場ができ,この磁場が勝手な方向を向いていた分子電流の中心軸の方向を,磁場の方向に揃える.揃えられた分子電流の方向は,外から与えた電流と同じ方向を向いている.鉄の分子の分布密度が一様であるときには,鉄の内部の隣りどうしの分子電流は互いに消しあって,巨視的には鉄の表面上の分子電流だけが働き,その巨視的平均値が磁化電流![]() として鉄の表面上に現れる.この磁化電流のつくる磁場が,ソレノイドの電流のつくる磁場と重ね合わさって,磁束密度が増大するというのがアンペールの考えである.物体に磁化電流が生じるとき,これを磁化といい,このように磁化を起こす物質を狭義の磁性体という5.2.
として鉄の表面上に現れる.この磁化電流のつくる磁場が,ソレノイドの電流のつくる磁場と重ね合わさって,磁束密度が増大するというのがアンペールの考えである.物体に磁化電流が生じるとき,これを磁化といい,このように磁化を起こす物質を狭義の磁性体という5.2.