


: マクスウェルの方程式
: マクスウェルの方程式と電磁波
: 磁性体中の静磁場
(5.2.5)あるいは(5.2.6)式で与えられるアンペールの法則は,定常的な伝導電流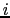 (
( )によってつくられる静磁場を規定する.(5.2.6)式の発散をとると,
)によってつくられる静磁場を規定する.(5.2.6)式の発散をとると,
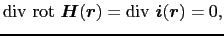 |
|
|
(5.3.14) |
となる.このことは,(5.2.6)式のアンペールの法則が定常電流の保存則と矛盾しないようにできていることを意味する.
静磁場を規定するガウスの法則は,時間的に変化する一般の磁場に対しても成立するが,一般の非定常電流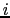 (
( ,
,  )によってつくられる磁場を規定する法則はどのように表されるであろうか?ガウスの法則の場合と同様に,(5.2.6)式のアンペールの法則の形をそのままに保って一般化すると,これは電荷保存則と明らかに矛盾する.そこでマクスウェルは,アンペールの法則を,
)によってつくられる磁場を規定する法則はどのように表されるであろうか?ガウスの法則の場合と同様に,(5.2.6)式のアンペールの法則の形をそのままに保って一般化すると,これは電荷保存則と明らかに矛盾する.そこでマクスウェルは,アンペールの法則を,
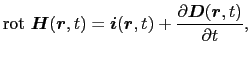 |
|
|
(5.3.15) |
のように一般化した.この右辺の追加項を変位電流という.(5.3.2)式が電荷保存則と矛盾しないことは,(5.3.2)式の両辺の発散をとり,一般化されたガウスの法則を用いれば,
のように証明される.すべての量が時間的に変化しないときには,(5.3.2)式の追加項は0となり,(5.3.2)式は(5.2.6)式に帰着する.マクスウェルによって一般化された(5.3.2)式を,アンペール・マクスウェルの法則という.
(5.3.2)式において,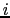 (
( , t) = 0とおいたとき,伝導電流がなくても変位電流が磁場をつくることに注意しよう.この変位電流が磁場をつくるという効果が,電磁波の存在を導く.
, t) = 0とおいたとき,伝導電流がなくても変位電流が磁場をつくることに注意しよう.この変位電流が磁場をつくるという効果が,電磁波の存在を導く.
Masashige Onoda
平成18年4月15日
![]() (
(![]() ,
, ![]() )によってつくられる磁場を規定する法則はどのように表されるであろうか?ガウスの法則の場合と同様に,(5.2.6)式のアンペールの法則の形をそのままに保って一般化すると,これは電荷保存則と明らかに矛盾する.そこでマクスウェルは,アンペールの法則を,
)によってつくられる磁場を規定する法則はどのように表されるであろうか?ガウスの法則の場合と同様に,(5.2.6)式のアンペールの法則の形をそのままに保って一般化すると,これは電荷保存則と明らかに矛盾する.そこでマクスウェルは,アンペールの法則を,
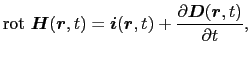
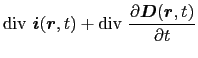
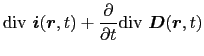
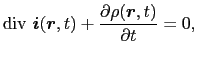
![]() (
(![]() , t) = 0とおいたとき,伝導電流がなくても変位電流が磁場をつくることに注意しよう.この変位電流が磁場をつくるという効果が,電磁波の存在を導く.
, t) = 0とおいたとき,伝導電流がなくても変位電流が磁場をつくることに注意しよう.この変位電流が磁場をつくるという効果が,電磁波の存在を導く.