


: 自由空間における電磁波
: マクスウェルの方程式と電磁波
: 変位電流
最終的に,物質中の電磁場を規定する基本法則は,次のようにまとめられる.
 誘電体中の静電場におけるガウスの法則
誘電体中の静電場におけるガウスの法則
電荷分布と電場とが時間的に変動する場合にまで一般化.
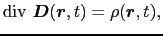 |
|
|
(5.4.17) |
 静磁場におけるガウスの法則
静磁場におけるガウスの法則
時間的に変動する磁場の場合にまで一般化.
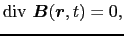 |
|
|
(5.4.18) |
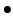 アンペール・マクスウェルの法則
アンペール・マクスウェルの法則
伝導電流および変位電流が磁場をつくることを表す.この変位電流は,一般の電荷保存則に矛盾しないように定常電流におけるアンペールの法則を一般化するにあたって,マクスウェルによって導入された.
 |
|
|
(5.4.19) |
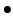 ファラデーの誘導法則
ファラデーの誘導法則
磁束密度の時間的変動に伴って空間に発生する誘導電場を与える.
 |
|
|
(5.4.20) |
以上の方程式を成分に分解すると8個の方程式が得られる.これに対して,右辺の および
および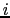 が既知の量であるとしても,8個の方程式に含まれる未知関数の数は,
が既知の量であるとしても,8個の方程式に含まれる未知関数の数は, ,
, ,
,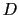 および
および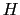 の各成分12個である.したがって,(5.4.1)〜(5.4.4)の方程式だけでは,解は一義的に決まらない.そこで,
の各成分12個である.したがって,(5.4.1)〜(5.4.4)の方程式だけでは,解は一義的に決まらない.そこで,
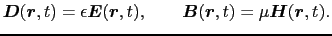 |
|
|
(5.4.21) |
という関係を設定する.ここで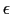 および
および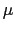 は,空間内に存在する物質の性質を反映する物質定数である.この関係は多くの物質について成立するが,強誘電体や強磁性体の場合には,
は,空間内に存在する物質の性質を反映する物質定数である.この関係は多くの物質について成立するが,強誘電体や強磁性体の場合には,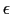 や
や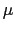 は定数とはならず,それぞれ電場の強さ
は定数とはならず,それぞれ電場の強さ および
および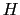 の関数になっている.また,異方性結晶の場合には,
の関数になっている.また,異方性結晶の場合には,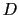 と
と の方向,あるいは
の方向,あるいは と
と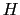 の方向が一致しないことがある.さらに,電磁場の時間的変化が激しいときには,(5.4.5)式の関係が成立しなくなる.しかしながら,
の方向が一致しないことがある.さらに,電磁場の時間的変化が激しいときには,(5.4.5)式の関係が成立しなくなる.しかしながら,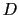 と
と ,
, と
と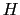 との間に関数関係が成立することは確かである.このことを考慮に入れて,マクスウェル方程式を
との間に関数関係が成立することは確かである.このことを考慮に入れて,マクスウェル方程式を と
と とだけで表せば,方程式の数が8個であるのに対して,未知関数は6個である.このときは方程式の数が多すぎるという心配が起こってくるかもしれないが,実際には問題はない.
とだけで表せば,方程式の数が8個であるのに対して,未知関数は6個である.このときは方程式の数が多すぎるという心配が起こってくるかもしれないが,実際には問題はない.
(5.4.3)式の両辺の発散をとってみよう.
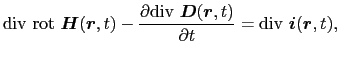 |
|
|
(5.4.22) |
における左辺の第1項は恒等的に0であり,また電荷保存則により,
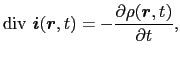 |
|
|
(5.4.23) |
であるから,(5.4.6)式は,
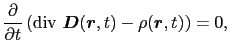 |
|
|
(5.4.24) |
となる.すなわち,div 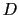 (
( ,
,  ) -
) -  (
( ,
,  )は時間的に一定な,場所
)は時間的に一定な,場所 の関数でなければならない.その初期条件として
の関数でなければならない.その初期条件として
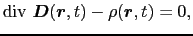 |
|
|
(5.4.25) |
と選べば,(5.4.1)式が成立する.
次に(5.5.4)式の両辺の発散をとってみる.
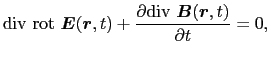 |
|
|
(5.4.26) |
における左辺の第1項は恒等的に0である.したがって,
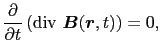 |
|
|
(5.4.27) |
となる.前と同様に,div  (
( ,
,  )は時間的に一定な,場所
)は時間的に一定な,場所 の関数でなければならない.その初期条件として,
の関数でなければならない.その初期条件として,
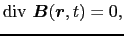 |
|
|
(5.4.28) |
と選べば(単磁荷が存在しない),(5.4.2)式が成立する.
マクスウェル方程式のうち,(5.4.1)式と(5.4.2)式とは初期条件として要求されるだけであり,電場 と磁場
と磁場 の時間的発展は残りの6個の方程式によって規定され,6個の未知関数にとって必要かつ十分な法則が与えられている.
の時間的発展は残りの6個の方程式によって規定され,6個の未知関数にとって必要かつ十分な法則が与えられている.



: 自由空間における電磁波
: マクスウェルの方程式と電磁波
: 変位電流
Masashige Onoda
平成18年4月15日
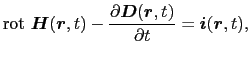
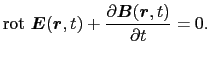
![]() および
および![]() が既知の量であるとしても,8個の方程式に含まれる未知関数の数は,
が既知の量であるとしても,8個の方程式に含まれる未知関数の数は,![]() ,
,![]() ,
,![]() および
および![]() の各成分12個である.したがって,(5.4.1)〜(5.4.4)の方程式だけでは,解は一義的に決まらない.そこで,
の各成分12個である.したがって,(5.4.1)〜(5.4.4)の方程式だけでは,解は一義的に決まらない.そこで,
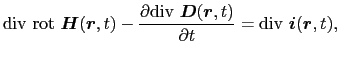
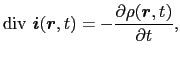
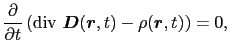
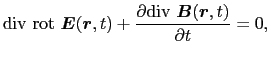
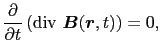
![]() と磁場
と磁場![]() の時間的発展は残りの6個の方程式によって規定され,6個の未知関数にとって必要かつ十分な法則が与えられている.
の時間的発展は残りの6個の方程式によって規定され,6個の未知関数にとって必要かつ十分な法則が与えられている.