


: 物理学B II
: マクスウェルの方程式と電磁波
: マクスウェルの方程式
電荷密度および電流密度の値が0であるような空間の領域を考え,この領域を自由空間と呼ぶことにする.この自由空間においては,マクスウェルの方程式は次のように表される.
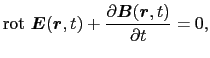 |
|
|
(5.5.29) |
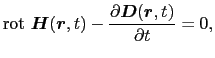 |
|
|
(5.5.30) |
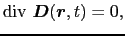 |
|
|
(5.5.31) |
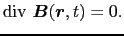 |
|
|
(5.5.32) |
ここで,
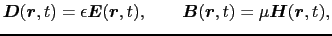 |
|
|
(5.5.33) |
が成立しているものと仮定する.自由空間が真空の場合には,(5.5.5)式で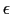 =
= 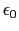 ,
,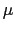 =
= 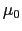 とおけばよい.
とおけばよい.
(5.5.1)式および(5.5.2)式からわかるように,磁場の時間的変化は電場を生み出し,また逆に電場の時間的変化によって磁場が生み出される.この電磁場は(5.5.3)式と(5.5.4)式を初期条件として満たしていなければならない.
(5.5.1)〜(5.5.4)式のマクスウェルの方程式に従う電磁場は,自由空間においてどのような運動の形態を示すであろうか?はじめに(5.5.1)式の回転をとる.
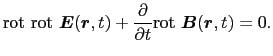 |
|
|
(5.5.34) |
ここで,(5.5.3),(5.5.5)式および
であることを用いれば,
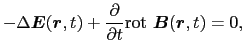 |
|
|
(5.5.35) |
となる.一方,(5.5.2),(5.5.5)式より,
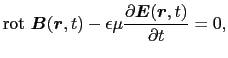 |
|
|
(5.5.36) |
である.(5.5.8)式を(5.5.7)式に代入すると,電場の満たす方程式が得られる.
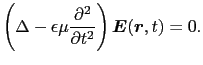 |
|
|
(5.5.37) |
同様に(5.5.8)式の回転をとり,(5.5.4)式の条件を用いると,磁場の満たす方程式は,
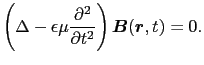 |
|
|
(5.5.38) |
(5.5.9),(5.5.10)式の解は,後で示されるように,自由空間内を伝播する波動を表すので,(5.5.9),(5.5.10)式を波動方程式という.電場と磁場がそれぞれ(5.5.9)式と(5.5.10)式の波動方程式を満たすことに基づいて,マクスウェルにより電磁波の存在が予言され,その後,ヘルツにより発見された.
電磁場の満たすマクスウェルの方程式の解が,実際に自由空間を伝播する波動になっていることを示すため,電場と磁場とが 方向にのみ変化している場合を考えよう.
方向にのみ変化している場合を考えよう.
このようにすると,たとえば(5.5.1)式は,
同様に,(5.5.2)式を成分に分けて,(5.5.5)と(5.5.11)式を用いると,
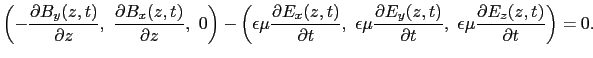 |
|
|
(5.5.41) |
(5.5.3)と(5.5.4)式とはそれぞれ,
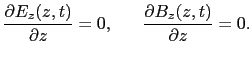 |
|
|
(5.5.42) |
(5.5.13)式の 成分と(5.5.14)式の第1式から,
成分と(5.5.14)式の第1式から,
 |
|
|
(5.5.43) |
(5.5.12)式の 成分と(5.5.14)式の第2式から,
成分と(5.5.14)式の第2式から,
 |
|
|
(5.5.44) |
(5.5.15),(5.5.16)式から,電場の 成分と磁場の
成分と磁場の 成分は,時間
成分は,時間 にもよらず,場所
にもよらず,場所 にもよらない定数であることがわかる.このような場は,静電場あるいは静磁場であるから,いまの場合,その定数を0にとって差し支えがない.
にもよらない定数であることがわかる.このような場は,静電場あるいは静磁場であるから,いまの場合,その定数を0にとって差し支えがない.
 |
|
|
(5.5.45) |
このことは,電場と磁場とが 軸に沿う方向の成分をもたず,それらの方向が
軸に沿う方向の成分をもたず,それらの方向が 軸に垂直な平面内にあることを示している.問題の取り扱いを簡単にするために,座標系の
軸に垂直な平面内にあることを示している.問題の取り扱いを簡単にするために,座標系の 軸を電場の方向に選ぼう.この座標系では,電場の
軸を電場の方向に選ぼう.この座標系では,電場の 方向の成分は0になるから,
方向の成分は0になるから,
 |
|
|
(5.5.46) |
とおくことができる.このとき,(5.5.12)式の 成分に関する方程式および(5.5.13)式の
成分に関する方程式および(5.5.13)式の 成分に関する方程式は,それぞれ,
成分に関する方程式は,それぞれ,
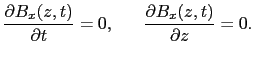 |
|
|
(5.5.47) |
すなわち,磁場の 方向の成分は
方向の成分は にも
にも にもよらない定数である.この定数を0に選ぶと,
にもよらない定数である.この定数を0に選ぶと,
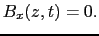 |
|
|
(5.5.48) |
こうして,磁場は 方向の成分のみをもつ.
方向の成分のみをもつ.
さて残されている方程式は,(5.5.12)式の 方向に関する方程式と(5.5.13)式の
方向に関する方程式と(5.5.13)式の 方向に関する方程式である.前者を
方向に関する方程式である.前者を で微分し,これに後者を代入すると,
で微分し,これに後者を代入すると,
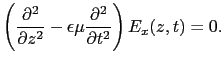 |
|
|
(5.5.49) |
同様にして,
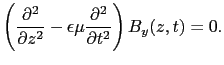 |
|
|
(5.5.50) |
ここで
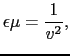 |
|
|
(5.5.51) |
とおくと, は速さの次元をもつ.
は速さの次元をもつ.
(5.5.21)式の解は,任意の関数 と
と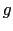 を用いて次のように表される.
を用いて次のように表される.
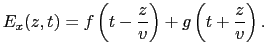 |
|
|
(5.5.52) |
実際,上式を(5.5.21)式に代入してみよう.
となるから(5.5.21)式が成立する.
一方,電場が(5.5.24)式で与えられているとき,磁場
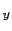 (
( ,
,  )は,
)は,
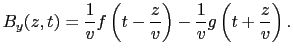 |
|
|
(5.5.53) |
で表される.
(5.5.24)式の解の性質を調べよう.(5.5.24)式の右辺の第1項の (
( -
-  /
/ )は,時間
)は,時間 の経過とともに,その形を保ちながら,速さ
の経過とともに,その形を保ちながら,速さ で
で の正の方向に移動していく.また第2項の
の正の方向に移動していく.また第2項の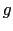 (
( +
+  /
/ )は,速さ
)は,速さ で
で の負の方向に進む.すなわち,電場は波のかたまりとなって,速さ
の負の方向に進む.すなわち,電場は波のかたまりとなって,速さ で伝播していく.ここで,
で伝播していく.ここで,
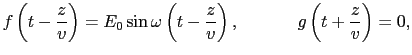 |
|
|
(5.5.54) |
とおいてみる.(5.5.26)式のように選んだとき,(5.5.24)式の電場と(5.5.25)式の磁場は,それぞれ,
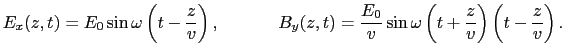 |
|
|
(5.5.55) |
ここで,
 |
|
|
(5.5.56) |
とおくと,(5.5.27)式は,
 |
|
|
(5.5.57) |
これはよく知られた の正の方向に進行する正弦波の波動関数である.(5.5.29)式の波動関数の形から,
の正の方向に進行する正弦波の波動関数である.(5.5.29)式の波動関数の形から,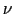 はこの正弦波の振動数であり,
はこの正弦波の振動数であり,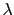 はその波長であることがわかる.これらの間には,
はその波長であることがわかる.これらの間には,
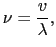 |
|
|
(5.5.58) |
の関係がある.ここで,
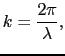 |
|
|
(5.5.59) |
とおこう.これは距離2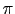 [m]のなかに含まれる波の数を表しており,波数と呼ばれる.角振動数
[m]のなかに含まれる波の数を表しており,波数と呼ばれる.角振動数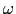 と波数
と波数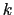 を用いると,(5.5.29)式は次のようになる.
を用いると,(5.5.29)式は次のようになる.
 |
|
|
(5.5.60) |
電磁波が真空中を伝わる速さ は,
は,
![$\displaystyle c
=
{1 \over{\sqrt{\epsilon_{0} \mu_{0}}}}
=
2.9979 \times 10^{8} [{\rm m/s}],$](img757.png) |
|
|
(5.5.61) |
となり,この値は真空中における光の速さに一致している.電磁波はその進行方向に垂直な平面内にのみ,その成分を持つので,光と同様に横波である.このことから,マクスウェルは,光は電磁波の一種に他ならないと結論した.



: 物理学B II
: マクスウェルの方程式と電磁波
: マクスウェルの方程式
Masashige Onoda
平成18年4月15日
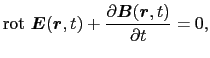
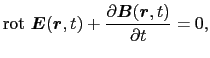
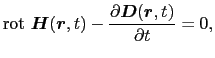
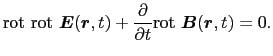
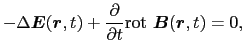
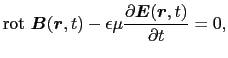
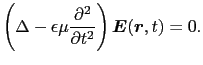
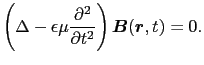
![]() 方向にのみ変化している場合を考えよう.
方向にのみ変化している場合を考えよう.
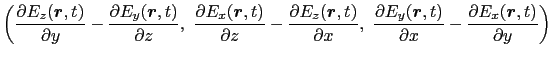
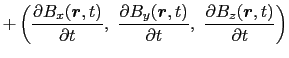
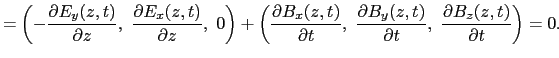
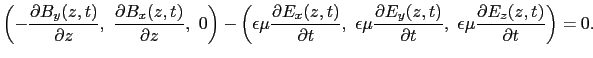
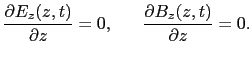
![]() 成分と(5.5.14)式の第1式から,
成分と(5.5.14)式の第1式から,
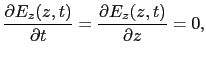
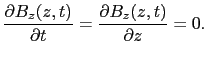
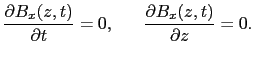
![]() 方向に関する方程式と(5.5.13)式の
方向に関する方程式と(5.5.13)式の![]() 方向に関する方程式である.前者を
方向に関する方程式である.前者を![]() で微分し,これに後者を代入すると,
で微分し,これに後者を代入すると,
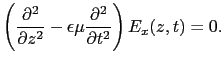
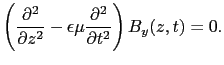
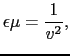
![]() と
と![]() を用いて次のように表される.
を用いて次のように表される.
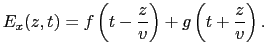
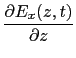
![$\displaystyle {\partial \over{\partial z}} \left [ f \left ( t - {z \over{v}} \right ) + g \left ( t + {z \over{v}} \right ) \right ]$](img744.png)
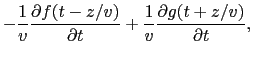
![$\displaystyle {\partial^{2} E_{x}(z, t) \over{\partial z^{2}}}
=
{1 \over{v^{2}...
...er{\partial t^{2}}} + {\partial^{2} g(t + z/v) \over{\partial t^{2}}} \right ],$](img746.png)
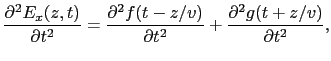
![]()
![]() (
(![]() ,
, ![]() )は,
)は,
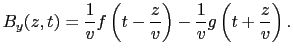
![]() (
(![]() -
- ![]() /
/![]() )は,時間
)は,時間![]() の経過とともに,その形を保ちながら,速さ
の経過とともに,その形を保ちながら,速さ![]() で
で![]() の正の方向に移動していく.また第2項の
の正の方向に移動していく.また第2項の![]() (
(![]() +
+ ![]() /
/![]() )は,速さ
)は,速さ![]() で
で![]() の負の方向に進む.すなわち,電場は波のかたまりとなって,速さ
の負の方向に進む.すなわち,電場は波のかたまりとなって,速さ![]() で伝播していく.ここで,
で伝播していく.ここで,
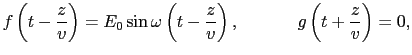
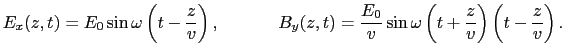


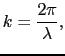

![]() は,
は,
![$\displaystyle c
=
{1 \over{\sqrt{\epsilon_{0} \mu_{0}}}}
=
2.9979 \times 10^{8} [{\rm m/s}],$](img757.png)