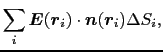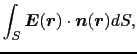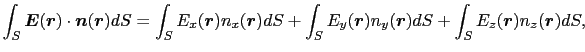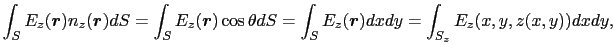: 積分形のガウスの法則
: 積分形のガウスの法則
: 積分形のガウスの法則
ここからしばらくは電磁気学をはじめとする物理学で頻繁に用いられる数学的手法を説明することになる.あまり馴染みのない演算子などが出て,ハードルが高く見えるかもしれない.戸惑うところもあるかと思うが,自ら学習して早く馴れてください.
二個のベクトル ,
, があるとき,そのスカラー積または内積
があるとき,そのスカラー積または内積
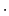
 を,
を,
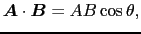 |
|
|
(1.2.19) |
と定義する.ここで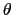 はベクトル間の角度である.(1.2.1)式は方向をもたず大きさだけで指定される量で,スカラー量という.因みに物理で現れる「仕事」は,力
はベクトル間の角度である.(1.2.1)式は方向をもたず大きさだけで指定される量で,スカラー量という.因みに物理で現れる「仕事」は,力  変位
変位 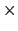 cos
cos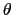 で与えられるが,これは変位の方向に射影した力の成分に変位をかけたものとして考えられる.
で与えられるが,これは変位の方向に射影した力の成分に変位をかけたものとして考えられる.
今,図1.5のような直交座標系を考える. ,
, ,
, 軸方向に関する基本ベクトルを,それぞれ
軸方向に関する基本ベクトルを,それぞれ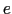
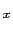 ,
,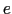
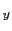 ,
,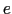
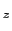 ,ベクトル
,ベクトル のそれぞれの座標軸の方向の成分を(
のそれぞれの座標軸の方向の成分を(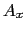 ,
,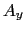 ,
,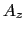 )とおくと,
)とおくと, は,
は,
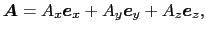 |
|
|
(1.2.20) |
と書ける.基本ベクトルには,
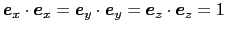 |
|
|
|
| |
|
|
(1.2.21) |
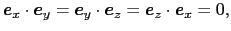 |
|
|
|
の関係があるので,(1.2.1)式は,
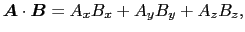 |
|
|
(1.2.22) |
とも表すことができる.
以上より,ある方向の単位ベクトルを と書くとき,スカラー積
と書くとき,スカラー積
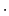
 はベクトル
はベクトル の
の 方向の成分を与えることがわかる.これを
方向の成分を与えることがわかる.これを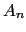 と書けば,
と書けば,
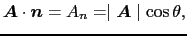 |
|
|
(1.2.23) |
となる.勿論,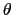 は
は と
と との間の角度である.また,
との間の角度である.また,
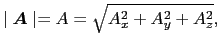 |
|
|
(1.2.24) |
である.
図 1.6:

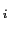 における面
における面 上の微小面
上の微小面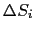 ,そこでの電場
,そこでの電場 (
( )と法線ベクトル
)と法線ベクトル (
(
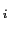 )
)
|
|
空間内のすべての点で電場 (
( )が与えられているとしよう(図1.6).空間内にある曲面
)が与えられているとしよう(図1.6).空間内にある曲面 を考え,その面上の点
を考え,その面上の点
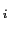 に
に に垂直に立てた単位ベクトルを
に垂直に立てた単位ベクトルを (
(
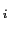 )とする.その曲面
)とする.その曲面 を細かく分割し,その上で
を細かく分割し,その上で (
(
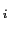 )
)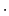
 (
(
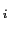 )の和をとってみよう.これは,
)の和をとってみよう.これは,
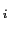 における面
における面 上の微小面の面積を
上の微小面の面積を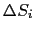 とすると,
とすると,
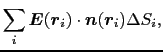 |
|
|
(1.2.25) |
の形で表される.上の微小面を無限小にしたとき,その極限値が分割の仕方に無関係に一定値に収束する場合には,
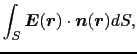 |
|
|
(1.2.26) |
と書くことができる.これを面積分という. (
( ),
), (
( )の成分を,それぞれ
)の成分を,それぞれ
と書けば,(1.2.8)式は,
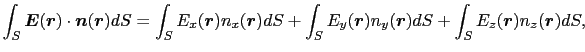 |
|
|
(1.2.27) |
となる.上式の最終項の積分は具体的には,
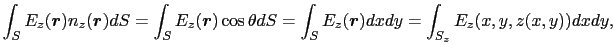 |
|
|
(1.2.28) |
と書ける.ここで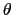 は
は (
( )と
)と 軸とのなす角度であり,cos
軸とのなす角度であり,cos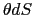 は図1.6で定義された
は図1.6で定義された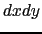 に等しい.また最終式では,局面
に等しい.また最終式では,局面 が
が =
=  (
( ,
,  )で与えられるとしたため,積分範囲を曲面
)で与えられるとしたため,積分範囲を曲面 から
から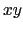 面へ投影したときの領域
面へ投影したときの領域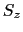 に変更している.
に変更している.



: 積分形のガウスの法則
: 積分形のガウスの法則
: 積分形のガウスの法則
Masashige Onoda
平成18年4月15日
![]() ,
,![]() があるとき,そのスカラー積または内積
があるとき,そのスカラー積または内積![]()
![]()
![]() を,
を,
![]() と書くとき,スカラー積
と書くとき,スカラー積![]()
![]()
![]() はベクトル
はベクトル![]() の
の![]() 方向の成分を与えることがわかる.これを
方向の成分を与えることがわかる.これを![]() と書けば,
と書けば,