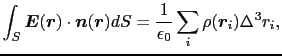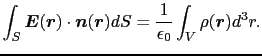

: 第2回演習問題
: 積分形のガウスの法則
: ベクトルのスカラー積と面積分
図 1.7:
点電荷 の位置ベクトル
の位置ベクトル
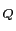 を中心とする球面および法線ベクトル
を中心とする球面および法線ベクトル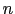
|
|
(1.1.7)式において,図1.7のような
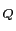 を中心とする半径
を中心とする半径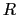 =
= 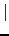
 -
- 
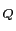
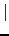 の球面を考えよう.球面に立てた単位法線ベクトル
の球面を考えよう.球面に立てた単位法線ベクトル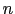 は半径の方向を向くので,
は半径の方向を向くので,
とおいてよい.したがって,
が得られる.ここで両辺に球の表面積4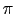
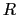
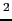 をかけると
をかけると
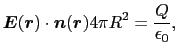 |
|
|
(1.2.29) |
となる.すなわち,球の中心におかれた点電荷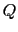 を中心として放射状に広がる電場を球面上で加え合わせたとき,その値は,球の中心にある電荷の値を
を中心として放射状に広がる電場を球面上で加え合わせたとき,その値は,球の中心にある電荷の値を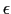
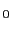 で割ったものに等しいことがわかる.
で割ったものに等しいことがわかる.
図 1.8:
点電荷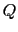 を囲む任意の閉曲面
を囲む任意の閉曲面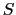 に関するガウスの法則の導出
に関するガウスの法則の導出
|
|
今度は,図1.8のような点電荷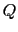 を囲む任意の閉曲面
を囲む任意の閉曲面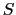 を考えてみよう.このときは,閉曲面
を考えてみよう.このときは,閉曲面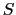 上にとった微小面
上にとった微小面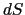 とその上の電場
とその上の電場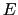 (
( )とは一般に直交していない.
)とは一般に直交していない.
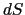 に立てた単位法線ベクトルを
に立てた単位法線ベクトルを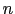 (
( )としよう.
)としよう.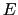 (
( )の
)の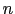 (
( )方向の成分は,
)方向の成分は,
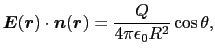 |
|
|
(1.2.30) |
となる.ここで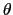 は
は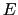 (
( )と
)と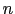 (
( )の間の角度を表す.ここで,微小面
)の間の角度を表す.ここで,微小面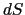 を点電荷
を点電荷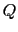 からみた立体角
からみた立体角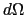 を1.1,
を1.1,
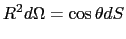 |
|
|
(1.2.31) |
として導入すると,(1.2.12)式は
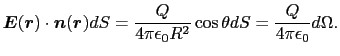 |
|
|
(1.2.32) |
したがって,
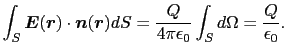 |
|
|
(1.2.33) |
すなわち,(1.2.11)式は点電荷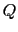 を囲む任意の閉曲面に対して成り立つ.
を囲む任意の閉曲面に対して成り立つ.
図 1.9:
点電荷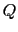 を囲まない任意の閉曲面
を囲まない任意の閉曲面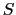 に関するガウスの法則の導出
に関するガウスの法則の導出
|
|
次に,図1.9に示すように,点電荷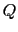 をその内部に含まない閉曲面
をその内部に含まない閉曲面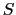 を考えよう.このときは,面積分を
を考えよう.このときは,面積分を
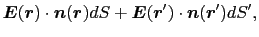 |
|
|
(1.2.34) |
のように分解して考えるとよい.今,
より,
となるので,
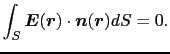 |
|
|
(1.2.35) |
これまでは,閉曲面として点電荷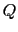 から引いた半直線が閉曲面
から引いた半直線が閉曲面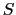 と二度以上交わらない場合を考えたが,それ以上交わる場合でも上式は成立する(証明略).
と二度以上交わらない場合を考えたが,それ以上交わる場合でも上式は成立する(証明略).
閉曲面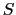 の内部に点電荷
の内部に点電荷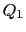 ,
,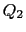 ,
,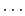 ,
,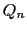 があり,その外部に点電荷
があり,その外部に点電荷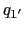 ,
,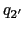 ,
,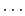 ,
,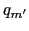 がある一般の場合を考えよう.このとき,これらの電荷が閉曲面
がある一般の場合を考えよう.このとき,これらの電荷が閉曲面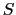 上の
上の なる場所に作る電場を,それぞれ
なる場所に作る電場を,それぞれ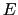
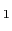 (
( ),
),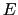
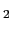 (
( ),
), ,
,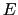
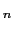 (
( )および
)および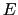
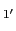 (
( ),
),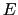
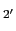 (
( ),
), ,
,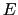
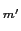 (
( )とする.このとき全電場は,
)とする.このとき全電場は,
(1.2.15)式,(1.2.17)式より,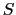 内にある点電荷からの寄与は残り,
内にある点電荷からの寄与は残り,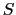 の外にある点電荷からの寄与は消える.
の外にある点電荷からの寄与は消える.
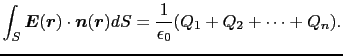 |
|
|
(1.2.36) |
これを積分形のガウスの法則という.
電荷が連続的に分布している場合には,空間を細かく分割し,それぞれの微小体積に番号を付け,場所
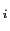 における電荷密度を
における電荷密度を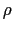 (
(
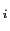 ),そこでの微小体積を
),そこでの微小体積を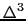

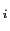 として計算を行えばよい.
として計算を行えばよい.
において,
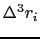
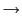 0の極限をとると
0の極限をとると
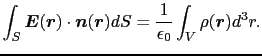 |
|
|
(1.2.37) |


: 第2回演習問題
: 積分形のガウスの法則
: ベクトルのスカラー積と面積分
Masashige Onoda
平成18年4月15日
![\includegraphics[scale=0.8, clip]{fig-1-2-3.eps}](img149.png)
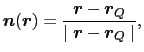
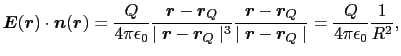
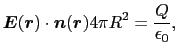
![]() に立てた単位法線ベクトルを
に立てた単位法線ベクトルを![]() (
(![]() )としよう.
)としよう.![]() (
(![]() )の
)の![]() (
(![]() )方向の成分は,
)方向の成分は,
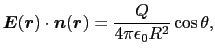
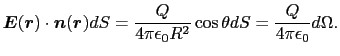
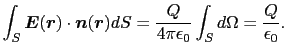
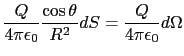
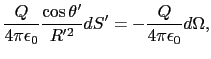
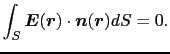
![]() から引いた半直線が閉曲面
から引いた半直線が閉曲面![]() と二度以上交わらない場合を考えたが,それ以上交わる場合でも上式は成立する(証明略).
と二度以上交わらない場合を考えたが,それ以上交わる場合でも上式は成立する(証明略).
![]() の内部に点電荷
の内部に点電荷![]() ,
,![]() ,
,![]() ,
,![]() があり,その外部に点電荷
があり,その外部に点電荷![]() ,
,![]() ,
,![]() ,
,![]() がある一般の場合を考えよう.このとき,これらの電荷が閉曲面
がある一般の場合を考えよう.このとき,これらの電荷が閉曲面![]() 上の
上の![]() なる場所に作る電場を,それぞれ
なる場所に作る電場を,それぞれ![]()
![]() (
(![]() ),
),![]()
![]() (
(![]() ),
),![]() ,
,![]()
![]() (
(![]() )および
)および![]()
![]() (
(![]() ),
),![]()
![]() (
(![]() ),
),![]() ,
,![]()
![]() (
(![]() )とする.このとき全電場は,
)とする.このとき全電場は,
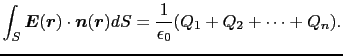
![]()
![]() における電荷密度を
における電荷密度を![]() (
(![]()
![]() ),そこでの微小体積を
),そこでの微小体積を![]()
![]()
![]() として計算を行えばよい.
として計算を行えばよい.