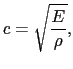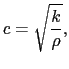: 第13回演習問題
: 波動
: 波動
図7.1のように,力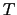 で引っ張られている,一様で線密度
で引っ張られている,一様で線密度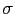 の弦の振動を考えよう.はじく前の弦の位置を
の弦の振動を考えよう.はじく前の弦の位置を 軸にとり,弦に垂直な方向の弦の変位を
軸にとり,弦に垂直な方向の弦の変位を (
( ,
,  )で表す.
)で表す.
 と
と +
+ 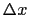 の間の微小部分PQに着目すると,PとQで隣接する部分から受ける力はいずれも
の間の微小部分PQに着目すると,PとQで隣接する部分から受ける力はいずれも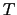 であるが,力の方向が僅かに異なる.図7.1のように角度を定めると,PQ部分の
であるが,力の方向が僅かに異なる.図7.1のように角度を定めると,PQ部分の 方向における運動方程式は,
方向における運動方程式は,
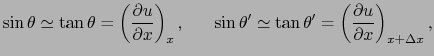 |
|
|
(7.1.1) |
である.ここで,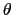 ,
,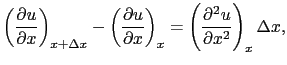 がどちらも微小ならば,
がどちらも微小ならば,
となる.また,
となるから,(7.1.1)式は,
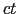 |
|
|
(7.1.2) |
と書ける.
一般に, を定数として,
を定数として,
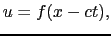 |
|
|
(7.1.3) |
のような形の微分方程式を一次元の波動方程式という.この方程式は, が
が -
-  の任意の関数,
の任意の関数,
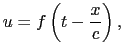 |
|
|
(7.1.4) |
ならば,
であるから満足する.(7.1.4)式は, = 0に
= 0に =
=  (
( )であった変位が,時間が
)であった変位が,時間が だけたった後には,距離
だけたった後には,距離 だけ
だけ 座標の増した位置に同じ変位が生じるという意味である.(7.1.4)式は,また,
座標の増した位置に同じ変位が生じるという意味である.(7.1.4)式は,また,
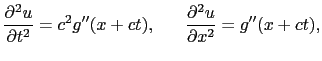 |
|
|
(7.1.5) |
と書くこともできる.この形にしてみると, = 0において
= 0において =
=  (
( )で表されている変位が,原点から
)で表されている変位が,原点から だけ離れた点では時間
だけ離れた点では時間 /
/ だけ遅れた時刻に生じる変位と等しいことがわかる.すなわち,(7.1.4)式で表される変位が一定の速さ
だけ遅れた時刻に生じる変位と等しいことがわかる.すなわち,(7.1.4)式で表される変位が一定の速さ で
で 軸の正の向きにそのまま伝わっていくわけで,これは波である.
軸の正の向きにそのまま伝わっていくわけで,これは波である.
同様にして, が
が +
+  の任意の関数,
の任意の関数,
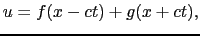 |
|
|
(7.1.6) |
であるときも,
となるので,(7.1.3)式を満たす.(7.1.6)式は波が速さ で
で 軸の負の向きに伝わる場合に相当する.
軸の負の向きに伝わる場合に相当する.
(7.1.4)式と(7.1.6)式より,
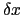 |
|
|
(7.1.7) |
で表される和も(7.1.3)式の解になることがわかる.これを重ね合せの原理という.
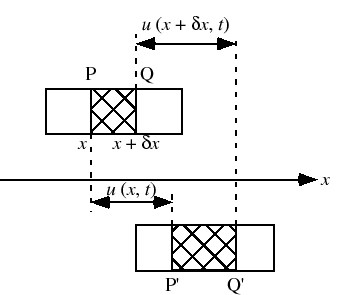
これまでの議論からわかるように,弦を伝わる波では,変位は波の伝わる方向に垂直である.これを横波という.波の伝わる速さ は,(7.1.2)と(7.1.3)式を比較することにより,
は,(7.1.2)と(7.1.3)式を比較することにより,
 |
|
|
(7.1.8) |
これは,媒質である弦を静止の位置に戻そうとする力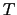 と媒質の慣性に比例する量
と媒質の慣性に比例する量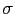 との比によって速さが決まることを示している.この関係は物体中を伝わる波について一般的に成り立つ.静止の位置に戻そうとする力が物体の弾性に起因する場合,その波を弾性波という.空気中の音波も,空気の体積弾性が関係しているから弾性波である.音波は縦波,すなわち各部分の変位が波の進む方向に起こる波で,このとき必ず密度変化を伴いながら波が進むので疎密波とも呼ばれる.
との比によって速さが決まることを示している.この関係は物体中を伝わる波について一般的に成り立つ.静止の位置に戻そうとする力が物体の弾性に起因する場合,その波を弾性波という.空気中の音波も,空気の体積弾性が関係しているから弾性波である.音波は縦波,すなわち各部分の変位が波の進む方向に起こる波で,このとき必ず密度変化を伴いながら波が進むので疎密波とも呼ばれる.
次に,密度 ,ヤング率
,ヤング率 の弾性材質でつくられた,断面積
の弾性材質でつくられた,断面積 の一様な棒の中を伝わる縦波の速さを求めてみよう.図7.2のように,棒の軸方向に
の一様な棒の中を伝わる縦波の速さを求めてみよう.図7.2のように,棒の軸方向に 軸をとる.波がない状態では,
軸をとる.波がない状態では, の位置にあった断面Pおよび
の位置にあった断面Pおよび +
+ 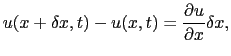 の位置にあった断面Qが,波のために時刻
の位置にあった断面Qが,波のために時刻 には,それぞれ
には,それぞれ +
+  (
( ,
,  )のP
)のP ,
, +
+ 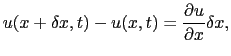 +
+  (
( +
+ 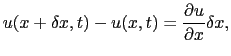 ,
,  )のQ
)のQ に移るとする.
に移るとする.
このときP Q
Q はPQよりも,
はPQよりも,
だけ長い.すなわち,P Q
Q の伸び歪みは
の伸び歪みは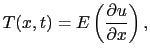 /
/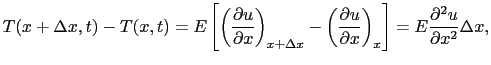 であり,断面P
であり,断面P にはたらく応力
にはたらく応力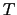 (
( ,
,  )は,
)は,
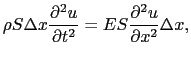 |
|
|
(7.1.9) |
となる.上式を導く際には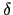
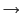 0の極限を考えた.今度は波のこないときのPQ間の長さ
0の極限を考えた.今度は波のこないときのPQ間の長さ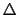
 は不変で,PQは常に有限の質量
は不変で,PQは常に有限の質量

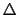
 をもつとする.時刻
をもつとする.時刻 においてPはP
においてPはP に移動しているが,P
に移動しているが,P とQ
とQ にはたらく応力の差は(7.1.9)式から,
にはたらく応力の差は(7.1.9)式から,
![$\displaystyle T(x + \Delta x, t) - T(x, t)
=
E \left [ \left ( {\partial u \ove...
...l x}} \right )_{x} \right ]
=
E {\partial^{2}u \over{\partial x^{2}}} \Delta x,$](img915.png) |
|
|
(7.1.10) |
となる.したがって,P Q
Q に関する運動方程式は,
に関する運動方程式は,
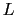 |
|
|
(7.1.11) |
と書ける.これより縦波の速さは,
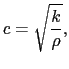 |
|
|
(7.1.12) |
となる.



: 第13回演習問題
: 波動
: 波動
Masashige Onoda
平成18年4月15日
![]() と
と![]() +
+ ![]() の間の微小部分PQに着目すると,PとQで隣接する部分から受ける力はいずれも
の間の微小部分PQに着目すると,PとQで隣接する部分から受ける力はいずれも![]() であるが,力の方向が僅かに異なる.図7.1のように角度を定めると,PQ部分の
であるが,力の方向が僅かに異なる.図7.1のように角度を定めると,PQ部分の![]() 方向における運動方程式は,
方向における運動方程式は,
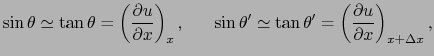
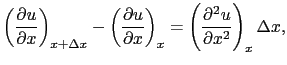 がどちらも微小ならば,
がどちらも微小ならば,
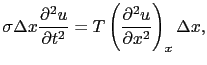
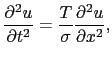
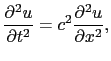
![]() を定数として,
を定数として,
 の任意の関数,
の任意の関数,
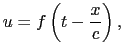
 だけ
だけ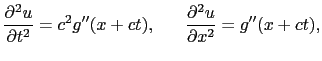
![]() が
が![]() +
+  の任意の関数,
の任意の関数,
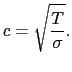
![]() は,(7.1.2)と(7.1.3)式を比較することにより,
は,(7.1.2)と(7.1.3)式を比較することにより,

![]() ,ヤング率
,ヤング率![]() の弾性材質でつくられた,断面積
の弾性材質でつくられた,断面積![]() の一様な棒の中を伝わる縦波の速さを求めてみよう.図7.2のように,棒の軸方向に
の一様な棒の中を伝わる縦波の速さを求めてみよう.図7.2のように,棒の軸方向に![]() 軸をとる.波がない状態では,
軸をとる.波がない状態では,![]() の位置にあった断面Pおよび
の位置にあった断面Pおよび![]() +
+ 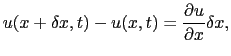 の位置にあった断面Qが,波のために時刻
の位置にあった断面Qが,波のために時刻![]() には,それぞれ
には,それぞれ![]() +
+ ![]() (
(![]() ,
, ![]() )のP
)のP![]() ,
,![]() +
+ 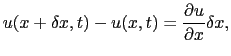 +
+ ![]() (
(![]() +
+ 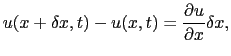 ,
, ![]() )のQ
)のQ![]() に移るとする.
に移るとする.
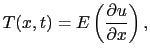 /
/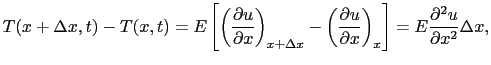 であり,断面P
であり,断面P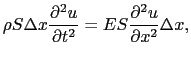
![$\displaystyle T(x + \Delta x, t) - T(x, t)
=
E \left [ \left ( {\partial u \ove...
...l x}} \right )_{x} \right ]
=
E {\partial^{2}u \over{\partial x^{2}}} \Delta x,$](img915.png)