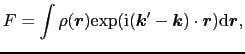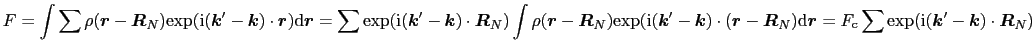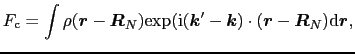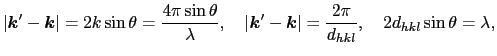: 結晶構造因子の計算
: 回折
: 結晶構造の決定
目次
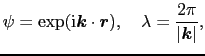 |
|
|
(1.5.17) |
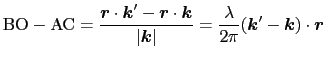 |
|
|
(1.5.18) |
行路差に伴う
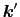 方向での波の位相差
方向での波の位相差
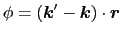 |
|
|
(1.5.19) |
対象中の電子の電荷分布
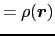
対象全体から
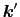 方向へ散乱された波の振幅は,重ね合わせの原理から,
方向へ散乱された波の振幅は,重ね合わせの原理から,
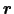 点の所での
点の所での
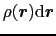 による散乱波の重ね合わせとなるはずである.→構造因子
による散乱波の重ね合わせとなるはずである.→構造因子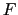
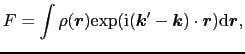 |
|
|
(1.5.20) |
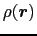 →
→
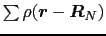 ;
;
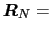
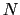 番目の単位胞の位置
番目の単位胞の位置
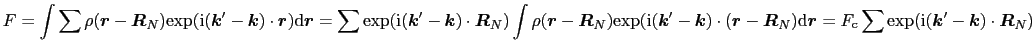 |
|
|
(1.5.21) |
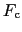 :結晶構造因子
:結晶構造因子
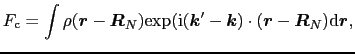 |
|
|
(1.5.22) |
各単位胞で散乱された波が最も強く強め合う方向→すべての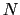 についてexpの中の変数が
についてexpの中の変数が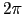 の整数倍
の整数倍
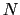 番目の単位胞の位置(1.2.1)式(
番目の単位胞の位置(1.2.1)式(
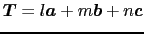 )より,ブラッグ反射の条件を得る.
)より,ブラッグ反射の条件を得る.
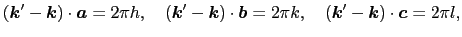 |
|
|
(1.5.23) |
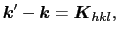 |
|
|
(1.5.24) |
(証明)
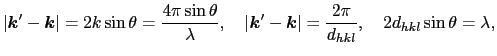 |
|
|
(1.5.25) |




: 結晶構造因子の計算
: 回折
: 結晶構造の決定
目次
Masashige Onoda
平成18年4月7日