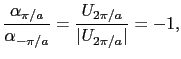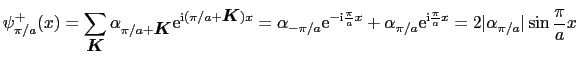: 半導体モデル
: 電子状態とバンド構造
: 強く束縛された電子の近似
目次
原子配列と一致した,摂動と見なせるほど弱い周期的ポテンシャル
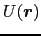 を導入する.逆格子ベクトル
を導入する.逆格子ベクトル
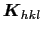 を用いて,
を用いて,
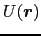 をフーリエ級数に展開する.
をフーリエ級数に展開する.
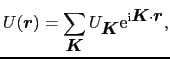 |
|
|
(3.5.48) |
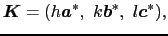 |
|
|
(3.5.49) |
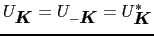 |
|
|
(3.5.50) |
固有関数
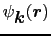 の
の
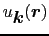 もフーリエ級数に展開する.
もフーリエ級数に展開する.
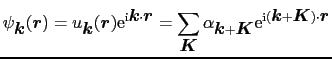 |
|
|
(3.5.51) |
上式は,結晶中で電子状態を記述する平面波が周期的ポテンシャル場の中でブラッグ反射を受けることを表す.
(5-1),(5-2)式をシュレーディンガー方程式に代入する.
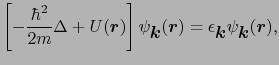 |
|
|
(3.5.52) |
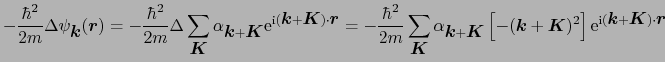 |
|
|
(3.5.53) |
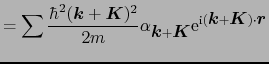 |
|
|
(3.5.54) |
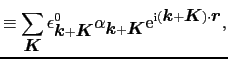 |
|
|
(3.5.55) |
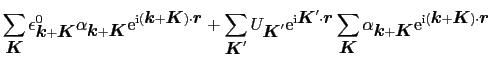 |
|
|
(3.5.56) |
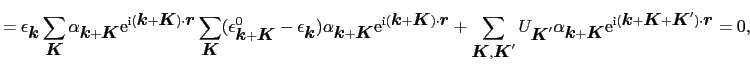 |
|
|
(3.5.57) |
上式に,
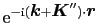 を掛けて積分する.
を掛けて積分する.
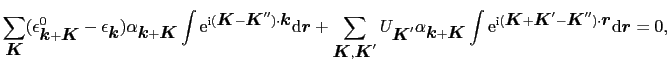 |
|
|
(3.5.58) |
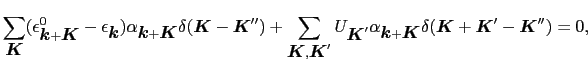 |
|
|
(3.5.59) |
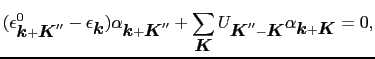 |
|
|
(3.5.60) |
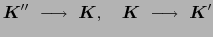 |
|
|
(3.5.61) |
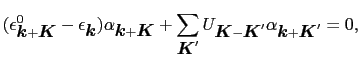 |
|
|
(3.5.62) |
上式は,1つの
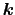 を指定したときに
を指定したときに
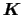 の数だけの連立方程式を与える.
の数だけの連立方程式を与える.
第2項の
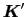 の和の中で1つの
の和の中で1つの
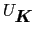 だけが重要である場合を考える.
だけが重要である場合を考える.
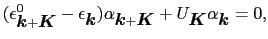 |
|
|
(3.5.63) |
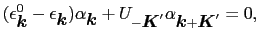 |
|
|
(3.5.64) |
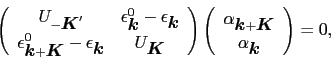 |
(3.5.65) |
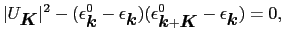 |
|
|
(3.5.66) |
![$\displaystyle \epsilon_{\mbox{\boldmath$k$}} = {1 \over{2}}\left[\epsilon_{\mbo...
...mbox{\boldmath$K$}}^{0})^{2} + 4\vert U_{\mbox{\boldmath$K$}}\vert^{2}}\right],$](img454.png) |
|
|
(3.5.67) |
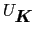 の影響の大きいのは
の影響の大きいのは
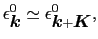 |
|
|
(3.5.68) |
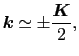 |
|
|
(3.5.69) |
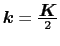 では,
では,
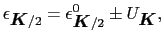 |
|
|
(3.5.70) |
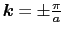 での様子を調べる.
での様子を調べる.
![$\displaystyle \epsilon_{\mbox{\boldmath$k$}}^{-} = {1 \over{2}}\left[2\epsilon_...
...t U_{{2\pi}/a}\vert^{2}}\right]
= \epsilon_{\pi/a}^{0} - \vert U_{2\pi/a}\vert,$](img461.png) |
|
|
(3.5.71) |
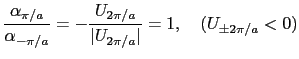 |
|
|
(3.5.72) |
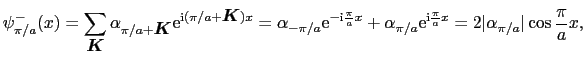 |
|
|
(3.5.73) |
![$\displaystyle \epsilon_{\mbox{\boldmath$k$}}^{+} = {1 \over{2}}\left[2\epsilon_...
...ert U_{2\pi/a}\vert^{2}}\right] = \epsilon_{\pi/a}^{0} + \vert U_{2\pi/a}\vert,$](img464.png) |
|
|
(3.5.74) |
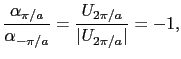 |
|
|
(3.5.75) |
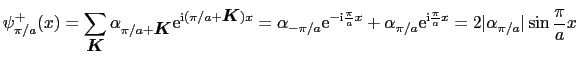 |
|
|
(3.5.76) |




: 半導体モデル
: 電子状態とバンド構造
: 強く束縛された電子の近似
目次
Masashige Onoda
平成18年4月7日
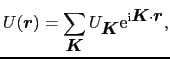
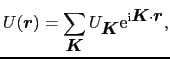
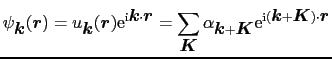
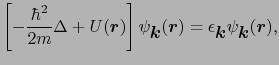
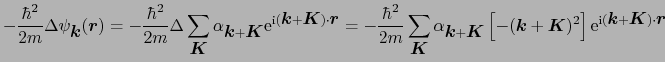
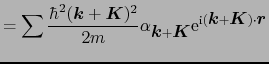
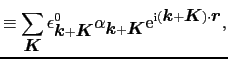
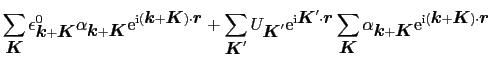
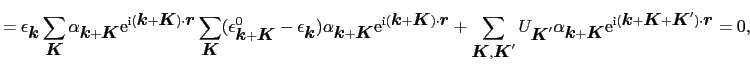
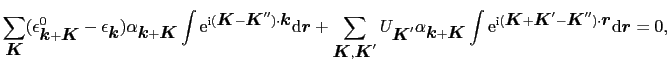
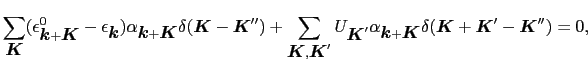
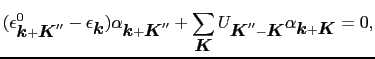
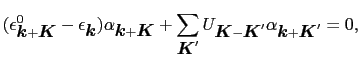
![]() の和の中で1つの
の和の中で1つの
![]() だけが重要である場合を考える.
だけが重要である場合を考える.
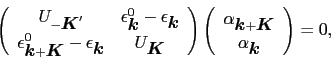
![$\displaystyle \epsilon_{\mbox{\boldmath$k$}} = {1 \over{2}}\left[\epsilon_{\mbo...
...mbox{\boldmath$K$}}^{0})^{2} + 4\vert U_{\mbox{\boldmath$K$}}\vert^{2}}\right],$](img454.png)
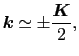
![$\displaystyle \epsilon_{\mbox{\boldmath$k$}}^{-} = {1 \over{2}}\left[2\epsilon_...
...t U_{{2\pi}/a}\vert^{2}}\right]
= \epsilon_{\pi/a}^{0} - \vert U_{2\pi/a}\vert,$](img461.png)
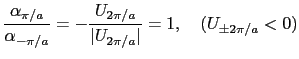
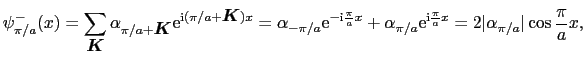
![$\displaystyle \epsilon_{\mbox{\boldmath$k$}}^{+} = {1 \over{2}}\left[2\epsilon_...
...ert U_{2\pi/a}\vert^{2}}\right] = \epsilon_{\pi/a}^{0} + \vert U_{2\pi/a}\vert,$](img464.png)