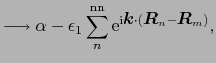: 弱い周期場
: 電子状態とバンド構造
: ブロッホの定理
目次
結晶中を動き回る電子状態(ブロッホ関数で表される状態)も,もとは自由原子の固有状態に由来する.
↓
原子間距離が大きい場合には,各原子核付近での電子の振る舞いは,自由原子のときの電子状態がある程度保存されているだろう.
ブロッホ関数は,各原子核を中心にした原子軌道の1次結合で近似できると考える.
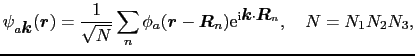 |
|
|
(3.4.34) |
 |
|
|
(3.4.35) |
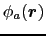 として方向性のないs軌道を考える.
として方向性のないs軌道を考える.
![$\displaystyle \epsilon_{\mbox{\boldmath$k$}} = \int{\rm d}\mbox{\boldmath$r$}\p...
... + U(\mbox{\boldmath$r$})\right]\psi_{\mbox{\boldmath$k$}}(\mbox{\boldmath$r$})$](img414.png) |
|
|
(3.4.36) |
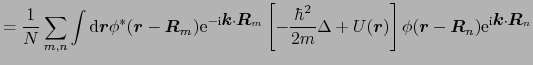 |
|
|
(3.4.37) |
![$\displaystyle = {1 \over{N}}\sum_{m, n}{\rm e}^{{\rm i}\mbox{\boldmath$k$}\cdot...
...\mbox{\boldmath$r$})\right]\phi(\mbox{\boldmath$r$} - \mbox{\boldmath$R$}_{n}),$](img416.png) |
|
|
(3.4.38) |
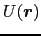 は結晶格子定数とともに周期的だから,
は結晶格子定数とともに周期的だから,
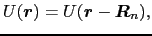 |
|
|
(3.4.39) |
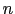 番目の原子について,自由原子の状態のときに働くポテンシャルエネルギー
番目の原子について,自由原子の状態のときに働くポテンシャルエネルギー
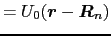
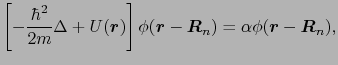 |
|
|
(3.4.40) |
![$\displaystyle \epsilon_{\mbox{\boldmath$k$}} = {1 \over{N}}\sum_{m, n}{\rm e}^{...
...(\mbox{\boldmath$r$})\right]\phi(\mbox{\boldmath$r$} - \mbox{\boldmath$R$}_{n})$](img421.png) |
|
|
(3.4.41) |
![$\displaystyle = \alpha + {1 \over{N}}\sum_{m, n}{\rm e}^{{\rm i}\mbox{\boldmath...
...ox{\boldmath$R$}_{n})\right]\phi(\mbox{\boldmath$r$} - \mbox{\boldmath$R$}_{n})$](img422.png) |
|
|
(3.4.42) |
![$\displaystyle = \alpha + {1 \over{N}}\sum_{m, n}{\rm e}^{{\rm i}\mbox{\boldmath...
...ox{\boldmath$R$}_{n})\right]\phi(\mbox{\boldmath$r$} - \mbox{\boldmath$R$}_{n})$](img422.png) |
|
|
(3.4.43) |
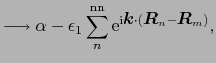 |
|
|
(3.4.44) |
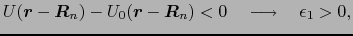 |
|
|
(3.4.45) |
(4-5)式を単純立方格子の場合について計算してみる.
最隣接格子点
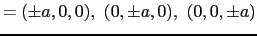
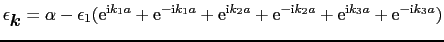 |
|
|
(3.4.46) |
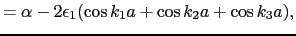 |
|
|
(3.4.47) |




: 弱い周期場
: 電子状態とバンド構造
: ブロッホの定理
目次
Masashige Onoda
平成18年4月7日
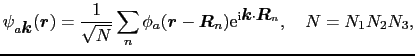
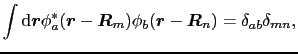
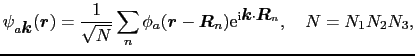
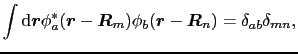
![$\displaystyle \epsilon_{\mbox{\boldmath$k$}} = \int{\rm d}\mbox{\boldmath$r$}\p...
... + U(\mbox{\boldmath$r$})\right]\psi_{\mbox{\boldmath$k$}}(\mbox{\boldmath$r$})$](img414.png)
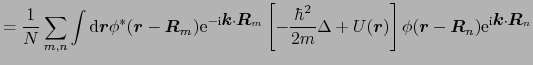
![$\displaystyle = {1 \over{N}}\sum_{m, n}{\rm e}^{{\rm i}\mbox{\boldmath$k$}\cdot...
...\mbox{\boldmath$r$})\right]\phi(\mbox{\boldmath$r$} - \mbox{\boldmath$R$}_{n}),$](img416.png)
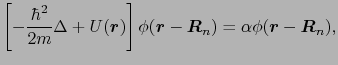
![$\displaystyle \epsilon_{\mbox{\boldmath$k$}} = {1 \over{N}}\sum_{m, n}{\rm e}^{...
...(\mbox{\boldmath$r$})\right]\phi(\mbox{\boldmath$r$} - \mbox{\boldmath$R$}_{n})$](img421.png)
![$\displaystyle = \alpha + {1 \over{N}}\sum_{m, n}{\rm e}^{{\rm i}\mbox{\boldmath...
...ox{\boldmath$R$}_{n})\right]\phi(\mbox{\boldmath$r$} - \mbox{\boldmath$R$}_{n})$](img422.png)
![$\displaystyle = \alpha + {1 \over{N}}\sum_{m, n}{\rm e}^{{\rm i}\mbox{\boldmath...
...ox{\boldmath$R$}_{n})\right]\phi(\mbox{\boldmath$r$} - \mbox{\boldmath$R$}_{n})$](img422.png)