



: 完全反磁性の現象論
: 超伝導と遷移金属酸化物
: エネルギーギャップ
目次
超伝導体の状態は温度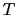 と外からかけた磁場
と外からかけた磁場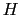 によって完全に決まるから,超伝導体の熱力学を作ることができる.まず,超伝導状態と常伝導状態の自由エネルギーを,温度
によって完全に決まるから,超伝導体の熱力学を作ることができる.まず,超伝導状態と常伝導状態の自由エネルギーを,温度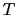 と磁場
と磁場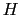 との関数として,それぞれ
との関数として,それぞれ
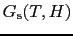 ,
,
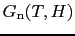 とおく.
とおく.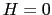 で
で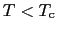 では超伝導状態が実現しているから,
では超伝導状態が実現しているから,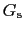 の方が
の方が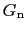 より小さい.磁場
より小さい.磁場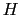 がかかると,超伝導状態では内部で磁場をゼロにするように表面に電流が流れ,そのための運動エネルギーが増加する.内部での磁場がゼロになるように電流が流れていることから,そのエネルギーを計算すると
がかかると,超伝導状態では内部で磁場をゼロにするように表面に電流が流れ,そのための運動エネルギーが増加する.内部での磁場がゼロになるように電流が流れていることから,そのエネルギーを計算すると
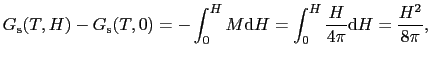 |
|
|
(7.3.2) |
となる.一方常伝導状態では,磁場がかかっても何も変化しないので
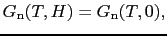 |
|
|
(7.3.3) |
である.臨界磁場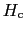 では,二つの相は釣り合うから,二つの自由エネルギーは等しくなければならない.すなわち
では,二つの相は釣り合うから,二つの自由エネルギーは等しくなければならない.すなわち
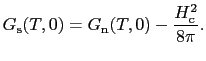 |
|
|
(7.3.4) |
これから二つの相のエントロピーを求めると,
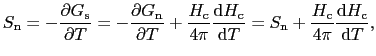 |
|
|
(7.3.5) |
となる.
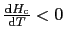 であるから,
であるから,
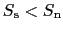 となる.エントロピーは,その系の無秩序の度合いを表しているから,超伝導状態の方が秩序だっており,何らかの意味での規則性が存在していることになる.
となる.エントロピーは,その系の無秩序の度合いを表しているから,超伝導状態の方が秩序だっており,何らかの意味での規則性が存在していることになる.
(7.3.4)式より磁場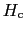 のときの超伝導から常伝導への転移では,
のときの超伝導から常伝導への転移では,
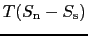 の熱量を発生することになり,潜熱を伴う1次の相転移であることがわかる.
の熱量を発生することになり,潜熱を伴う1次の相転移であることがわかる.
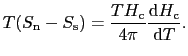 |
|
|
(7.3.6) |
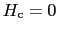 すなわち
すなわち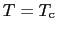 では,上式はゼロになり潜熱はない.
では,上式はゼロになり潜熱はない.
比熱は
となり,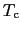 では
では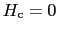 とおいて
とおいて
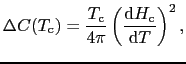 |
|
|
(7.3.7) |
となる.こうして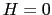 での超伝導と常伝導の相転移は潜熱はなく,比熱が不連続になる2次の相転移であることがわかった.
での超伝導と常伝導の相転移は潜熱はなく,比熱が不連続になる2次の相転移であることがわかった.
Masashige Onoda
平成18年4月7日
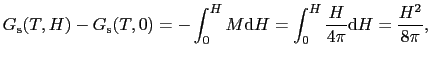
![]() のときの超伝導から常伝導への転移では,
のときの超伝導から常伝導への転移では,
![]() の熱量を発生することになり,潜熱を伴う1次の相転移であることがわかる.
の熱量を発生することになり,潜熱を伴う1次の相転移であることがわかる.
![$\displaystyle \Delta C = C_{\rm s} - C_{\rm n} = T\frac{\partial S}{\partial T}...
... c}}{{\rm d}T^{2}} + \left(\frac{{\rm d}H_{\rm c}}{{\rm d}T}\right)^{2}\right],$](img1197.png)