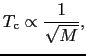 |
(7.6.37) |
結晶中の格子振動は波となって結晶中を動き(たとえば音波),その波は波数ベクトル
![]() と振動の方向
と振動の方向
![]() で指定される.格子振動を記述するには,各々の波がどのような振動状態にあるかを指定すればよいが,それには
で指定される.格子振動を記述するには,各々の波がどのような振動状態にあるかを指定すればよいが,それには
![]() ,
,![]() に対して一つの整数
に対して一つの整数![]() を与えればよい.電磁波を量子化して光子(フォトン)というように,この波に対応してフォノンを考え,
を与えればよい.電磁波を量子化して光子(フォトン)というように,この波に対応してフォノンを考え,![]() を
を
![]() ,
,![]() というモードのフォノンの数という.
というモードのフォノンの数という.
電子と格子振動との相互作用は,運動量
![]() の電子がフォノン
の電子がフォノン
![]() を吸収して
を吸収して
![]() に移るか,フォノン
に移るか,フォノン
![]() を放出して
を放出して
![]() に移ることからなる.フォノンの振動数
に移ることからなる.フォノンの振動数
![]() は
は
![]() に比例するというデバイ模型を用いるが,この比例定数(波の速度)がイオンの質量
に比例するというデバイ模型を用いるが,この比例定数(波の速度)がイオンの質量![]() の平方根に逆比例する.この模型では,波数
の平方根に逆比例する.この模型では,波数
![]() には上限があり(大体イオン間隔の逆数程度),それに相当して振動数にも上限がある.この上限を
には上限があり(大体イオン間隔の逆数程度),それに相当して振動数にも上限がある.この上限を
![]() と書き,これに対応するエネルギー
と書き,これに対応するエネルギー
![]() を温度に換算したものをデバイ温度
を温度に換算したものをデバイ温度
![]() という.
という.
同位元素効果によって,超伝導の主役は電子とフォノンとの相互作用であることは確かになったが,これから超伝導状態がどのようなものであるかを明らかにするのは難しい問題であった.この問題に対して重要な一歩をしるしたのが,1956年のクーパーの考えであった.
金属内電子は温度ゼロでフェルミ球の内部に詰まっているが,いまその外側に2個の電子を付け加えたとする.この2個の電子の間に引力が働いていると,2個の電子は運動量空間の1点に静止しているよりも,あちらこちらを絡み合って動き回った方が,エネルギーが低くなり一種の束縛状態を作る.束縛状態というのは,たとえば水素原子2個を考えればよい.この2個はバラバラに動き回るより2個が一緒になって動いた方がエネルギーが低くなり,水素分子を作る.いまの場合は運動量空間での電子であるため,具体的なイメージは正確には描けないが,普通の空間でも2個の電子は水素分子と同じようにある平均距離を保って一緒に動いていると考えてよい.この束縛状態にある2個の電子をクーパー対と呼ぶ.以上ではフェルミ球の外に2個の電子を付け加えたと考えたが,この2個の電子は外から付け加えたものである必要はない.フェルミ面上から2個の電子をとり,その運動を考えたとしてもよい.すると束縛状態ができるため,全体のエネルギーはフェルミ球のままでいるより低くなるから,こういうクーパー対が1組だけでなく,できるだけたくさんの対ができた方がエネルギー的に得をするはずである.したがってフェルミ球はどんどん崩れ,フェルミ球は不安定になる.こうしてフェルミ面上の電子の間に引力が働くと,フェルミ球は崩れて新しい基底状態ができるはずで,これを超伝導状態に対応させてよさそうである.したがってあとの問題は,クーパーが2電子に対して行った計算を,非常に多数の電子に対して行うことと,クーパー対の原因になる引力を,電子とフォノンとの相互作用から作ることになる.
このことを実際に示したのがBCSである.BCSはまず引力を電子フォノン相互作用から次のように作り出した.まず運動量
![]() の電子がフォノン
の電子がフォノン
![]() を放出して
を放出して
![]() に変わる.次に第2の電子
に変わる.次に第2の電子
![]() がそのフォノンを吸収して
がそのフォノンを吸収して
![]() に変わる.この最初と最後の状態を比べると,
に変わる.この最初と最後の状態を比べると,
![]() という電子対が
という電子対が
![]() に変わっており,フォノンには何の変化もない.この結果だけを見ると,電子どうしの衝突であり,電子の間の相互作用である.これと順番を逆にした過程もあり,この両方を合せたものをフォノンによって誘起された相互作用と呼ぶ.実際この相互作用を計算してみると,二つの電子のエネルギーがフェルミエネルギーからフォノンの平均エネルギー(
に変わっており,フォノンには何の変化もない.この結果だけを見ると,電子どうしの衝突であり,電子の間の相互作用である.これと順番を逆にした過程もあり,この両方を合せたものをフォノンによって誘起された相互作用と呼ぶ.実際この相互作用を計算してみると,二つの電子のエネルギーがフェルミエネルギーからフォノンの平均エネルギー(
![]() )以上離れていなければ,引力になることがわかった.BCSはこの相互作用をさらに簡単化して,エネルギーがフェルミエネルギーから
)以上離れていなければ,引力になることがわかった.BCSはこの相互作用をさらに簡単化して,エネルギーがフェルミエネルギーから
![]() 以内にあるすべての電子の間では,一定の引力が働いているとした.ただしこの相互作用だけでは,すべての金属が超伝導を示すことになって事実に反するので,これとクーロン反発力を考えて,フォノンによる引力がクーロン反発力より大きい金属が超伝導を示し,そうでないものは超伝導にならないと考えた.
以内にあるすべての電子の間では,一定の引力が働いているとした.ただしこの相互作用だけでは,すべての金属が超伝導を示すことになって事実に反するので,これとクーロン反発力を考えて,フォノンによる引力がクーロン反発力より大きい金属が超伝導を示し,そうでないものは超伝導にならないと考えた.
BCSはこの引力を用いて,クーパーが2電子に対して用いたクーパー対の考えを,多電子系に対して適用した.その結果,普通のフェルミ球で表される常伝導状態と違った状態が基底状態として出現し,そのときの常伝導状態に比べてのエネルギーの低下は,1電子あたり
温度が上がると,クーパー対がだんだん壊れていき,それにつれてエネルギーギャップの値もだんだん小さくなる.このギャップがゼロになる温度が転移温度で,