



: 中間状態
: 超伝導と遷移金属酸化物
: BCS理論の概要
目次
超伝導体の表面に平行な磁場がかかっている場合を考える.磁場は表面からある深さまでしか入り込まず,この深さが磁場の侵入長に相当する.第1種超伝導体ではこの長さはロンドン侵入長と一般に異なる値をもつので,これを改めて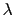 と書く.電流
と書く.電流
 も表面の近くだけで流れていると考えられる.そこで表面に近い点をとり,そこでの電流密度が磁場によってどう変化するかを考えてみる.
も表面の近くだけで流れていると考えられる.そこで表面に近い点をとり,そこでの電流密度が磁場によってどう変化するかを考えてみる.
 に影響を与える範囲は,点
に影響を与える範囲は,点
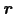 から距離
から距離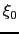 以内にある部分である.磁場の代わりにベクトルポテンシャルを用いると,
以内にある部分である.磁場の代わりにベクトルポテンシャルを用いると,
 は
は
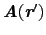 を
を
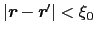 の範囲で積分したものと考えてよい.
の範囲で積分したものと考えてよい.
さて
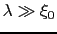 の場合は,この範囲では
の場合は,この範囲では
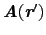 は一定の値をもち,したがって
は一定の値をもち,したがって
 は
は
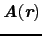 に比例することになる.これがロンドン方程式であり
に比例することになる.これがロンドン方程式であり
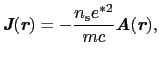 |
|
|
(7.7.41) |
と書ける.
一方逆の場合,
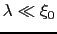 では,上の
では,上の
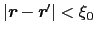 の範囲のうち磁場がゼロにならないのは
の範囲のうち磁場がゼロにならないのは
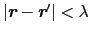 の部分だけである.したがって,
の部分だけである.したがって,
 への寄与は(7.7.1)式に比べると,
への寄与は(7.7.1)式に比べると,
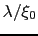 倍だけ小さくなるだろう.したがって
倍だけ小さくなるだろう.したがって
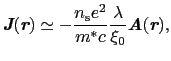 |
|
|
(7.7.42) |
と表される.これとマクスウェル方程式
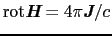 とを組み合わせて,
とを組み合わせて,
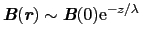 (
(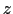 は表面に垂直な方向)という形をしているとすると
は表面に垂直な方向)という形をしているとすると
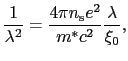 |
|
|
(7.7.43) |
となる.ロンドンの侵入長を用いると
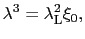 |
|
|
(7.7.44) |
と書ける.したがって第1種超伝導体では,磁場の侵入長は
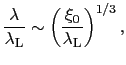 |
|
|
(7.7.45) |
となる.
Masashige Onoda
平成18年4月7日
![]() の場合は,この範囲では
の場合は,この範囲では
![]() は一定の値をもち,したがって
は一定の値をもち,したがって
![]() は
は
![]() に比例することになる.これがロンドン方程式であり
に比例することになる.これがロンドン方程式であり
![]() では,上の
では,上の
![]() の範囲のうち磁場がゼロにならないのは
の範囲のうち磁場がゼロにならないのは
![]() の部分だけである.したがって,
の部分だけである.したがって,
![]() への寄与は(7.7.1)式に比べると,
への寄与は(7.7.1)式に比べると,
![]() 倍だけ小さくなるだろう.したがって
倍だけ小さくなるだろう.したがって