



: 付近における振舞い
: 第2種超伝導体
: 磁気的性質
目次
いま超伝導体に強い磁場をかけ,磁場をだんだん弱くしていくと,ある磁場で超伝導を示すようになるが,このときまず試料の一部分が超伝導になる.このときの磁場が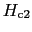 であり,超伝導の核ができる磁場といってもよい.
であり,超伝導の核ができる磁場といってもよい.
上記のような状況の下では,秩序パラメーターは非常に小さく,またベクトルポテンシャルは外からの磁場だけで決められると考えてよい.すなわち(7.5.5)式は,
となり,また(7.5.4)式は
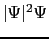 を無視して,
を無視して,
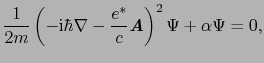 |
|
|
(7.10.54) |
と書ける.この式は,一様な磁場の下での自由電子に対するシュレーディンガー方程式と同じであるから,そのときの知識を利用して解くことができる.磁場の方向を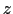 方向にとると,このときの自由電子の運動は
方向にとると,このときの自由電子の運動は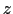 方向には自由に動き
方向には自由に動き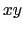 面内では円運動をする.この円運動の角振動数は
面内では円運動をする.この円運動の角振動数は
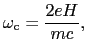 |
|
|
(7.10.55) |
で与えられる.これがサイクロトロン運動と呼ばれるものである.このときの量子力学的なエネルギーの値が(7.10.3)式の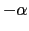 でなければならない.したがって,
でなければならない.したがって,
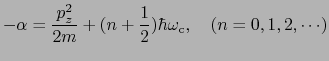 |
|
|
(7.10.56) |
で与えられる.特に最小のエネルギーは,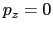 ,
,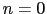 で与えられ,
で与えられ,
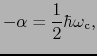 |
|
|
(7.10.57) |
となる.これが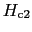 を決める式である.すなわち,(7.10.3)式の解である
を決める式である.すなわち,(7.10.3)式の解である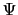 がある点のまわりだけ大きく,その点から離れたところでは非常に小さくなるためには,
がある点のまわりだけ大きく,その点から離れたところでは非常に小さくなるためには,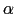 と
と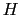 とは(7.10.6)式という関係を満たしていなければならない.
とは(7.10.6)式という関係を満たしていなければならない.
一方,熱力学的な臨界磁場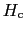 は(7.5.11)式で与えられているから,
は(7.5.11)式で与えられているから,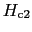 と
と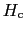 の関係は(7.5.17)式の
の関係は(7.5.17)式の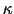 を用いて
を用いて
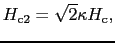 |
|
|
(7.10.58) |
と書けることがわかる.
こうして決めた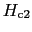 が
が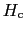 より小さければ,磁場を減少させていく途中で,
より小さければ,磁場を減少させていく途中で,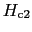 より前に
より前に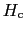 になるから,そこで試料全体が超伝導状態になり,完全なマイスナ−効果を示す.これが第1種超伝導体である.逆に
になるから,そこで試料全体が超伝導状態になり,完全なマイスナ−効果を示す.これが第1種超伝導体である.逆に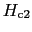 の方が
の方が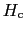 より大きければ,試料の一部だけが超伝導状態になり,試料の電気抵抗はゼロであるが,完全なマイスナ−効果は示さない.これが第2種超伝導体である.
より大きければ,試料の一部だけが超伝導状態になり,試料の電気抵抗はゼロであるが,完全なマイスナ−効果は示さない.これが第2種超伝導体である.
ある物質が第1種の超伝導体であるか,第2種の超伝導体であるかは,その物質の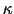 によって定まることになる.すなわち
によって定まることになる.すなわち
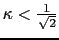 ならば第1種,
ならば第1種,
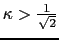 ならば第2種ということになる.
ならば第2種ということになる.




: 付近における振舞い
: 第2種超伝導体
: 磁気的性質
目次
Masashige Onoda
平成18年4月7日
![]() は(7.5.11)式で与えられているから,
は(7.5.11)式で与えられているから,![]() と
と![]() の関係は(7.5.17)式の
の関係は(7.5.17)式の![]() を用いて
を用いて
![]() が
が![]() より小さければ,磁場を減少させていく途中で,
より小さければ,磁場を減少させていく途中で,![]() より前に
より前に![]() になるから,そこで試料全体が超伝導状態になり,完全なマイスナ−効果を示す.これが第1種超伝導体である.逆に
になるから,そこで試料全体が超伝導状態になり,完全なマイスナ−効果を示す.これが第1種超伝導体である.逆に![]() の方が
の方が![]() より大きければ,試料の一部だけが超伝導状態になり,試料の電気抵抗はゼロであるが,完全なマイスナ−効果は示さない.これが第2種超伝導体である.
より大きければ,試料の一部だけが超伝導状態になり,試料の電気抵抗はゼロであるが,完全なマイスナ−効果は示さない.これが第2種超伝導体である.
![]() によって定まることになる.すなわち
によって定まることになる.すなわち
![]() ならば第1種,
ならば第1種,
![]() ならば第2種ということになる.
ならば第2種ということになる.