


: 過酸化脂肪ラジカル
: 電子スピン共鳴による有機物年代測定
: 電子スピン共鳴による有機物年代測定
目次
図 4.15:
熱分解によるラジカルの生成と最終生成物への化学反応模式図
|
|
有機物が酸化反応などによって分解する際に,不対電子を持つラジカルが生じる.分解反応が一定の反応定数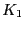 で進行してラジカルが生じ,さらに反応定数
で進行してラジカルが生じ,さらに反応定数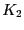 でより安定な分解生成物へと反応するなら,図4.15のような3つのレベルを摸式的に考えることができる.この場合,反応は
でより安定な分解生成物へと反応するなら,図4.15のような3つのレベルを摸式的に考えることができる.この場合,反応は
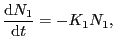 |
|
|
(4.5.3) |
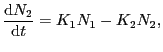 |
|
|
(4.5.4) |
と表わされる.ここで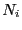 は有機物の量である.時間ゼロ(
は有機物の量である.時間ゼロ(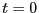 )で,
)で,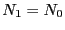 ,
,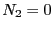 とすると,ラジカル濃度は次式で表わすことができる.
とすると,ラジカル濃度は次式で表わすことができる.
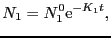 |
|
|
(4.5.5) |
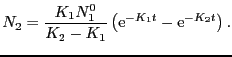 |
|
|
(4.5.6) |
ここで年代値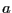 の有機ラジカルの量を
の有機ラジカルの量を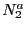 とおくと
とおくと
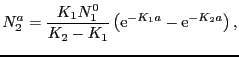 |
|
|
(4.5.7) |
となる.(4.5.1)と(4.5.2)式は放射性元素の壊変と娘核種の生成および壊変の場合と同じ式である.
不飽和脂肪酸に酸素が反応してできる過酸化脂肪ラジカルなど,一般的に化学反応による劣化の速度定数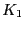 ,
,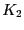 は,図4.15に示すようなエネルギー状態を考えると,反応の活性化エネルギー
は,図4.15に示すようなエネルギー状態を考えると,反応の活性化エネルギー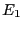 ,
,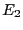 を用いることにより,
を用いることにより,
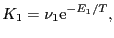 |
|
|
(4.5.8) |
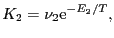 |
|
|
(4.5.9) |
と表わされる.ここで,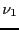 ,
,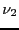 は定数(振動子強度に対応する)である.
は定数(振動子強度に対応する)である.
ラジカル濃度に対する一般解は,(4.5.3)と(4.5.4)式で与えられた.年代測定では,未知の年代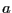 におけるラジカル濃度(4.5.5)式がわかっており,その後のラジカル濃度の増大から,
におけるラジカル濃度(4.5.5)式がわかっており,その後のラジカル濃度の増大から,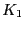 ,
,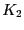 ,
,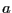 を評価する必要がある.室温でのラジカル濃度の増大を検出することは通常は容易ではないので,温度を上昇させて化学反応の速度を早めることにより年代値を求める.実験室での温度上昇が,時間進行速度を加速する「タイムマシン」の役割をするわけである.新しい温度で反応定数が,
を評価する必要がある.室温でのラジカル濃度の増大を検出することは通常は容易ではないので,温度を上昇させて化学反応の速度を早めることにより年代値を求める.実験室での温度上昇が,時間進行速度を加速する「タイムマシン」の役割をするわけである.新しい温度で反応定数が,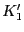 と
と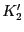 になったとする.(4.5.1),(4.5.2)式を新しい境界条件
になったとする.(4.5.1),(4.5.2)式を新しい境界条件
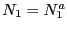 ,
,
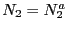 の下で解くと
の下で解くと
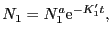 |
|
|
(4.5.10) |
![$\displaystyle N_{2} = \frac{K_{1}'N_{1}^{a}{\rm e}^{K_{1}'a}}{K_{2}' - K_{1}'}\...
...rm e}^{(-K_{1}' + K_{2}')a - K_{2}t}\right] + N_{2}^{a}{\rm e}^{K_{2}'(a - t)}.$](img401.png) |
|
|
(4.5.11) |
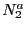 で規格化したラジカル濃度は,
で規格化したラジカル濃度は,
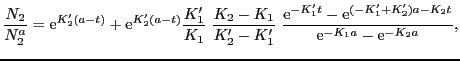 |
|
|
(4.5.12) |
となる.これから
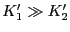 か
か
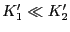 の場合には容易に求められる.
の場合には容易に求められる.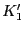 および
および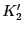 の温度依存性をアーレニウスプロットすれば活性化エネルギー
の温度依存性をアーレニウスプロットすれば活性化エネルギー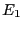 ,
,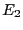 ,
,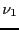 ,
,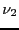 も求められる.直線部を外挿すると室温での
も求められる.直線部を外挿すると室温での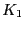 ,
,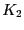 を評価できる.
を評価できる.
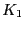 ,
,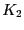 の大きさを変えた場合の例を,図4.16に摸式的に示した.
の大きさを変えた場合の例を,図4.16に摸式的に示した.
図 4.16:
反応定数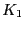 ,
,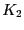 によるラジカル生成量の計算例.
によるラジカル生成量の計算例.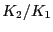 をパラメーターとして,単位時間の生成量で規格化している.放射平衡,永年平衡の場合の放射能値の積分値になっている.
をパラメーターとして,単位時間の生成量で規格化している.放射平衡,永年平衡の場合の放射能値の積分値になっている.
|
|
図 4.17:
(a)ポテトチップスと(b)紙のESRスペクトル.いずれも単一のESR信号ではない.
|
|
実際にはラジカル濃度の減衰は,(4.5.2)式のように単純とは限らないが,多くの場合,これらの式でその現象を説明でき,或る範囲内で年代値を求め得るものと考えられる.図4.16にラジカル量を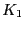 ,
,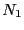 で規格化して示す.
で規格化して示す.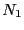 が十分に大きい場合,
が十分に大きい場合,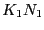 はほぼ一定と考えてよい(
はほぼ一定と考えてよい(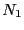 の減衰は無視できる).
の減衰は無視できる).
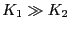 の場合は単純な飽和曲線になる.ラジカル生成曲線の立ち上りから
の場合は単純な飽和曲線になる.ラジカル生成曲線の立ち上りから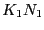 が,飽和または減衰から
が,飽和または減衰から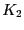 が求められる.
微分形表現は,放射平衡,永年平衡と考え方が同じであるがESRで検出できるのは,積分値の
が求められる.
微分形表現は,放射平衡,永年平衡と考え方が同じであるがESRで検出できるのは,積分値の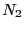 のみであることに注意する必要がある.以下の各節では,代表的な例について,これらの式に基づいた考察を行う.
のみであることに注意する必要がある.以下の各節では,代表的な例について,これらの式に基づいた考察を行う.



: 過酸化脂肪ラジカル
: 電子スピン共鳴による有機物年代測定
: 電子スピン共鳴による有機物年代測定
目次
Masashige Onoda
平成18年4月11日
![]() ,
,![]() は,図4.15に示すようなエネルギー状態を考えると,反応の活性化エネルギー
は,図4.15に示すようなエネルギー状態を考えると,反応の活性化エネルギー![]() ,
,![]() を用いることにより,
を用いることにより,
![]() におけるラジカル濃度(4.5.5)式がわかっており,その後のラジカル濃度の増大から,
におけるラジカル濃度(4.5.5)式がわかっており,その後のラジカル濃度の増大から,![]() ,
,![]() ,
,![]() を評価する必要がある.室温でのラジカル濃度の増大を検出することは通常は容易ではないので,温度を上昇させて化学反応の速度を早めることにより年代値を求める.実験室での温度上昇が,時間進行速度を加速する「タイムマシン」の役割をするわけである.新しい温度で反応定数が,
を評価する必要がある.室温でのラジカル濃度の増大を検出することは通常は容易ではないので,温度を上昇させて化学反応の速度を早めることにより年代値を求める.実験室での温度上昇が,時間進行速度を加速する「タイムマシン」の役割をするわけである.新しい温度で反応定数が,![]() と
と![]() になったとする.(4.5.1),(4.5.2)式を新しい境界条件
になったとする.(4.5.1),(4.5.2)式を新しい境界条件
![]() ,
,
![]() の下で解くと
の下で解くと
![]() ,
,![]() の大きさを変えた場合の例を,図4.16に摸式的に示した.
の大きさを変えた場合の例を,図4.16に摸式的に示した.
![]() ,
,![]() で規格化して示す.
で規格化して示す.![]() が十分に大きい場合,
が十分に大きい場合,![]() はほぼ一定と考えてよい(
はほぼ一定と考えてよい(![]() の減衰は無視できる).
の減衰は無視できる).
![]() の場合は単純な飽和曲線になる.ラジカル生成曲線の立ち上りから
の場合は単純な飽和曲線になる.ラジカル生成曲線の立ち上りから![]() が,飽和または減衰から
が,飽和または減衰から![]() が求められる.
微分形表現は,放射平衡,永年平衡と考え方が同じであるがESRで検出できるのは,積分値の
が求められる.
微分形表現は,放射平衡,永年平衡と考え方が同じであるがESRで検出できるのは,積分値の![]() のみであることに注意する必要がある.以下の各節では,代表的な例について,これらの式に基づいた考察を行う.
のみであることに注意する必要がある.以下の各節では,代表的な例について,これらの式に基づいた考察を行う.