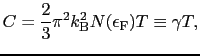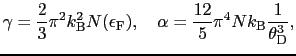: ブロッホの定理
: 電子状態とバンド構造
: 固体における電子状態
目次
「価電子を取り出した正電荷をもつ原子心をぬりつぶし,それによるポテンシャル中を価電子が自由に動き回る」(金属の価電子=伝導電子)Drudeによる固体電子論の基礎的考察に使われた.
一様なポテンシャル中での電子に関するシュレーディンガー方程式
エネルギースペクトル:放物線型
エネルギー等高線:球型
電子のつまった最高の準位=フェルミ準位
 空間におけるフェルミ準位上でのエネルギー等高線=フェルミ面
空間におけるフェルミ準位上でのエネルギー等高線=フェルミ面
波動関数に対する周期的境界条件
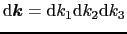 の体積要素の中に含まれる状態数
の体積要素の中に含まれる状態数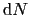 :
:
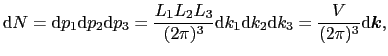 |
|
|
(3.2.4) |
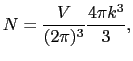 |
|
|
(3.2.5) |
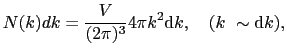 |
|
|
(3.2.6) |
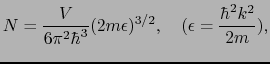 |
|
|
(3.2.7) |
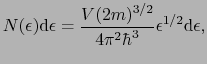 |
|
|
(3.2.8) |
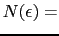 状態密度(スピン自由度 2倍)
状態密度(スピン自由度 2倍)
総数 の電子を収容したときのフェルミ波数とフェルミエネルギー
の電子を収容したときのフェルミ波数とフェルミエネルギー
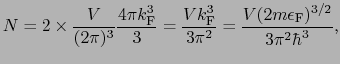 |
|
|
(3.2.9) |
原子が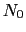 個あり,各原子が
個あり,各原子が 個の価電子を供出した場合
個の価電子を供出した場合
 |
|
|
(3.2.10) |
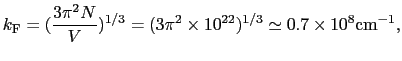 |
|
|
(3.2.11) |
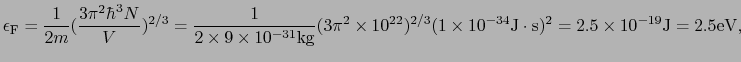 |
|
|
(3.2.12) |
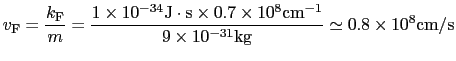 |
|
|
(3.2.13) |
※ 古典論
エネルギーの最も低い状態では電子はすべて静止している.有限温度での電子の平均速度は
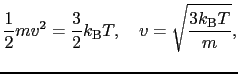 |
|
|
(3.2.14) |
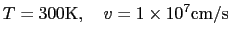 |
|
|
(3.2.15) |
フェルミ面上の電子は基底状態でありながら,上記の値よりも高速で動いている.(パウリ原理による)
有限温度における電子の振る舞い
分布関数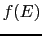 (エネルギー
(エネルギー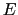 の量子状態に存在する電子の平均数)に基づいて考える.
の量子状態に存在する電子の平均数)に基づいて考える.
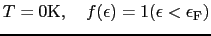 |
|
|
(3.2.16) |
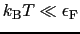 の条件
の条件
励起可能な電子 = フェルミ面近傍の電子(
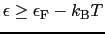 )
)
フェルミ球の外で
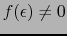 となる領域 =
となる領域 =
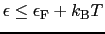 有限温度における分布関数
有限温度における分布関数
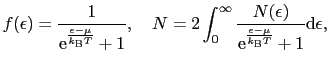 |
|
|
(3.2.17) |
比熱の計算
縮退した電子系のもつ内部エネルギー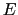
![$\displaystyle \langle E \rangle = \int{\rm d}\epsilon\cdot2\epsilon N(\epsilon)...
...T)^{2}[{{\rm d}(\epsilon N(\epsilon)) \over{{\rm d}\epsilon}}]_{\epsilon = \mu}$](img391.png) |
|
|
(3.2.18) |
電子比熱
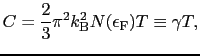 |
|
|
(3.2.19) |
金属の全比熱
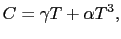 |
|
|
(3.2.20) |
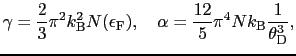 |
|
|
(3.2.21) |




: ブロッホの定理
: 電子状態とバンド構造
: 固体における電子状態
目次
Masashige Onoda
平成18年4月7日
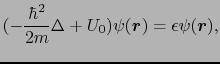
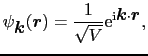
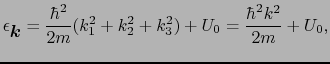
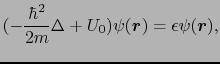
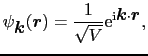
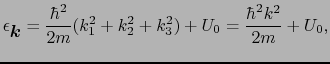
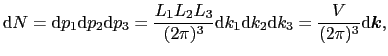
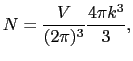
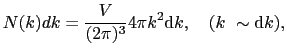
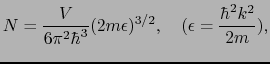
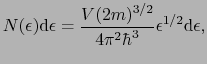
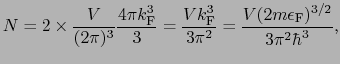
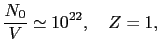
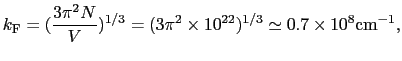
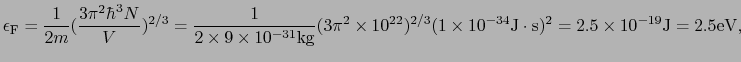
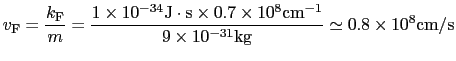
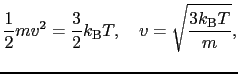
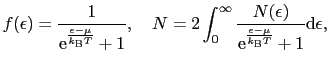
![$\displaystyle \langle E \rangle = \int{\rm d}\epsilon\cdot2\epsilon N(\epsilon)...
...T)^{2}[{{\rm d}(\epsilon N(\epsilon)) \over{{\rm d}\epsilon}}]_{\epsilon = \mu}$](img391.png)