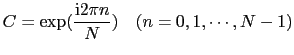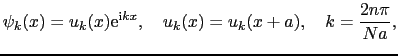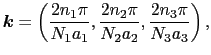: 強く束縛された電子の近似
: 電子状態とバンド構造
: 自由電子モデル
目次
格子定数a,結晶の長さNaの1次元系を考える.
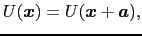 |
|
|
(3.3.22) |
このポテンシャル中でのシュレーディンガー方程式を解く.
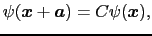 |
|
|
(3.3.23) |
すべての格子点は同等→どの格子点でも電子の発見確率は等しい
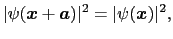 |
|
|
(3.3.24) |
すなわち,
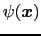 と
と
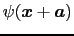 は同一であるか,異なっていても位相因子
は同一であるか,異なっていても位相因子
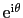 だけでなければならない.周期的境界条件より,
だけでなければならない.周期的境界条件より,
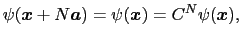 |
|
|
(3.3.25) |
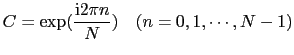 |
|
|
(3.3.26) |
したがって次の関数(ブロッホ関数)を用いればよい.
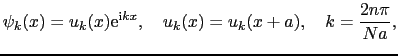 |
|
|
(3.3.27) |
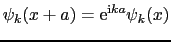 |
|
|
(3.3.28) |
格子定数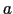 だけずれるごとに位相が
だけずれるごとに位相が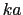 だけずれる.
だけずれる.
3次元の場合も同様である.
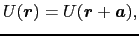 |
|
|
(3.3.29) |
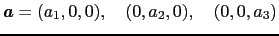 |
|
|
(3.3.30) |
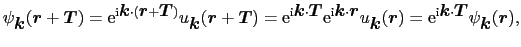 |
|
|
(3.3.31) |
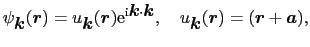 |
|
|
(3.3.32) |
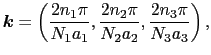 |
|
|
(3.3.33) |
ブロッホの条件式




: 強く束縛された電子の近似
: 電子状態とバンド構造
: 自由電子モデル
目次
Masashige Onoda
平成18年4月7日