 |
(7.4.8) |
 |
 |
|||
 |
|||
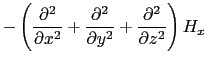 |
いま半無限に広がった超伝導体を考え,その表面を![]() 平面にとり,外からの磁場は表面に平行とし,その方向を
平面にとり,外からの磁場は表面に平行とし,その方向を![]() にとる.磁場
にとる.磁場
![]() は表面に垂直な
は表面に垂直な![]() 方向だけで変化するから,(7.4.7)式の
方向だけで変化するから,(7.4.7)式の![]() 成分をとって(
成分をとって(
![]() )
)
ロンドンの考え方は簡単で,実際の超伝導体には合わない点が多い.たとえば不純物の量が多くて,電子の平均自由行路が短い試料では,磁場の侵入長は不純物の量によって変化するが,ロンドンの理論ではこのようなことは説明できない.これを打開するために,ピパード(A. B. Pippard)はコヒーレンス長という考えを提唱した.
コヒーレンス長![]() というのは,超伝導体の中で電子が記憶を保って走る距離のようなもので,ある点の電子はその点のまわりの距離
というのは,超伝導体の中で電子が記憶を保って走る距離のようなもので,ある点の電子はその点のまわりの距離![]() のことを感じているといってもよい.したがって,ある点の電流
のことを感じているといってもよい.したがって,ある点の電流
![]() も,その点のまわりの距離
も,その点のまわりの距離![]() の範囲の磁場の影響を受けるはずである.
の範囲の磁場の影響を受けるはずである.
これに対してロンドン方程式では,同じ点の磁場だけで電流が決まってしまう.磁場が![]() 程度の距離では大きく変化していなければ,ある点のまわりの距離
程度の距離では大きく変化していなければ,ある点のまわりの距離![]() の範囲の磁場は一定とみなすことができロンドン方程式は正しいが,そうでないときは正しくない.磁場が変化する長さは大体
の範囲の磁場は一定とみなすことができロンドン方程式は正しいが,そうでないときは正しくない.磁場が変化する長さは大体
![]() と考えてよいから,ロンドン方程式は
と考えてよいから,ロンドン方程式は
![]() のときは正しいが,その逆の極限,
のときは正しいが,その逆の極限,
![]() のときは正しくないと考えられる.ピパードはこれらのことを考慮に入れて,
のときは正しくないと考えられる.ピパードはこれらのことを考慮に入れて,
こうして超伝導体には特徴的な長さが二つあることになる.一つはロンドンの侵入長
![]() であり,もう一つはコヒーレンス長
であり,もう一つはコヒーレンス長![]() である.
である.![]() の大きさを評価してみよう.
の大きさを評価してみよう.
まず純粋の試料について考える.超伝導体の励起エネルギーには![]() というギャップが存在する.このことは運動量空間における電子の分布がエネルギーにして
というギャップが存在する.このことは運動量空間における電子の分布がエネルギーにして![]() の程度の幅で乱れていることを意味する.電子はフェルミエネルギー
の程度の幅で乱れていることを意味する.電子はフェルミエネルギー
![]() まで詰まっているから,それに相当する運動量を
まで詰まっているから,それに相当する運動量を![]() と書くと,
と書くと,![]() というエネルギーの乱れは,運動量にすると
というエネルギーの乱れは,運動量にすると
![]() 程度の乱れになる.ハイゼンベルグの不確定性原理によると,運動量で
程度の乱れになる.ハイゼンベルグの不確定性原理によると,運動量で![]() という乱れがあることは,普通の空間では
という乱れがあることは,普通の空間では
![]() という不確定性があることになり,電子はこの程度の長さの範囲に広がっていると考えられる.したがって,この
という不確定性があることになり,電子はこの程度の長さの範囲に広がっていると考えられる.したがって,この![]() が純粋な超伝導体のコヒーレンス長
が純粋な超伝導体のコヒーレンス長![]() を与えることになる.さらに有効質量
を与えることになる.さらに有効質量![]() ,フェルミ面上での電子の速さ
,フェルミ面上での電子の速さ![]() を用いて
を用いて
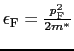 ,
,
![]() と書くと,
と書くと,
不純物を含んだ試料では,電子は不純物に散乱されて記憶を失う.したがってコヒーレンス長は純粋な試料の値より短くなる.不純物による散乱の目安は,平均自由行路![]() で与えられるが,不純物量が多くなり,
で与えられるが,不純物量が多くなり,![]() になると,
になると,![]() は
は![]() と同じ程度になるだろう.
と同じ程度になるだろう.
AlやSnのような普通の金属では,有効質量![]() は自由電子の質量に近く,
は自由電子の質量に近く,
![]() とすると,
とすると,
![]() は500 [Å]の程度になる.これに対してフェルミ面における電子の速さは
は500 [Å]の程度になる.これに対してフェルミ面における電子の速さは![]() [cm/s]程度であり,
[cm/s]程度であり,![]() は
は![]() [Å]に達する.したがって,
[Å]に達する.したがって,
![]() でロンドン方程式は使えない.これに対して遷移金属やその化合物では
でロンドン方程式は使えない.これに対して遷移金属やその化合物では![]() は大きく,したがって
は大きく,したがって
![]() も大きくなり
も大きくなり![]() [Å]程度になる.
[Å]程度になる.![]() は
は![]() [cm/s],
[cm/s],![]() は
は![]() [K]のため
[K]のため![]() も大きく,
も大きく,![]() は非常に小さくなる.すなわち
は非常に小さくなる.すなわち
![]() で,ロンドン方程式がよくあてはまる.
で,ロンドン方程式がよくあてはまる.
![]() を第1種超伝導体,
を第1種超伝導体,
![]() を第2種超伝導体とよぶ.
を第2種超伝導体とよぶ.