



: BCS理論の概要
: 超伝導と遷移金属酸化物
: 完全反磁性の現象論
目次
特に第2種超伝導体の熱力学的性質,磁気的性質をうまく記述する方程式が1950年にギンツブルグ(V. L. Ginzburg)とランダウ(L. D. Landau)によって提唱された.
超伝導と常伝導との転移は,磁場のないときは2次の相転移である.これを現象論的にとらえるにはオーダーパラメーターを用いると便利で,エネルギーギャップ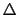 あるいは超伝導電子数
あるいは超伝導電子数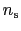 がそれに相当する.すなわち複素数である
がそれに相当する.すなわち複素数である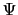 という量を考え,
という量を考え,
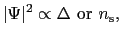 |
|
|
(7.5.20) |
とおく.磁場がないときの自由エネルギーは,
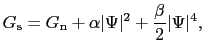 |
|
|
(7.5.21) |
で表される.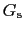 ,
,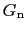 は,それぞれ超伝導状態,常伝導状態における自由エネルギーである.さらに磁場があるときの
は,それぞれ超伝導状態,常伝導状態における自由エネルギーである.さらに磁場があるときの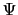 の空間的な変化を考慮に入れて,自由エネルギーの中に
の空間的な変化を考慮に入れて,自由エネルギーの中に
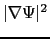 の項を加える.この項は量子力学における運動エネルギーの形と同じなので,
の項を加える.この項は量子力学における運動エネルギーの形と同じなので,
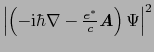 と書き換える.ここで
と書き換える.ここで
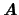 は磁場があるときの効果である.また反磁性の効果(7.3.1)式も含めれば,自由エネルギーは
は磁場があるときの効果である.また反磁性の効果(7.3.1)式も含めれば,自由エネルギーは
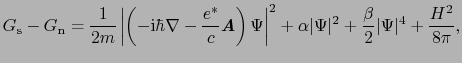 |
|
|
(7.5.22) |
と書ける.この式に対して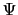 ,
,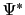 および
および
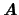 に関する変分をとると,
に関する変分をとると,
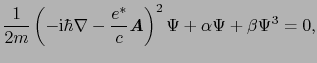 |
|
|
(7.5.23) |
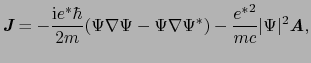 |
|
|
(7.5.24) |
を得る.
以下では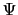 を量子力学的な波動関数と考え,
を量子力学的な波動関数と考え,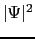 はその点における超伝導電子の密度
はその点における超伝導電子の密度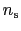 に等しいと考える.磁場ゼロで電流のない場合,すなわち
に等しいと考える.磁場ゼロで電流のない場合,すなわち
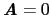 ,
,
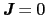 の場合を考える.このときは
の場合を考える.このときは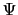 の場所による変化
の場所による変化
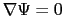 であるから,そのときの
であるから,そのときの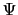 を
を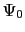 と書くと(7.5.4)式は
と書くと(7.5.4)式は
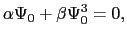 |
|
|
(7.5.25) |
となる.したがって
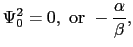 |
|
|
(7.5.26) |
となる.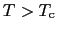 で
で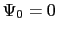 ,
,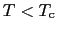 で
で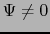 となるためには,
となるためには,
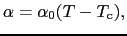 |
|
|
(7.5.27) |
であり,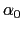 は
は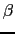 とともに温度によらない正の定数であればよいことがわかる.すなわち,
とともに温度によらない正の定数であればよいことがわかる.すなわち,
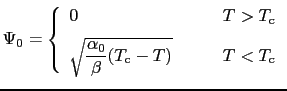 |
|
|
(7.5.28) |
となり,エネルギーギャップ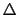 の
の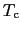 付近での振舞いに一致する.(7.5.2)式に(7.5.7)式の有限解を代入すると
付近での振舞いに一致する.(7.5.2)式に(7.5.7)式の有限解を代入すると
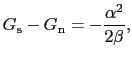 |
|
|
(7.5.29) |
となり,これから
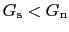 であるためには
であるためには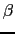 は正でなければならない.(7.5.10)式を(7.3.1)式と比べると臨界磁場は
は正でなければならない.(7.5.10)式を(7.3.1)式と比べると臨界磁場は
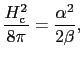 |
|
|
(7.5.30) |
と書けることになる.(7.5.8)式を入れれば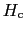 の温度変化を再現できる.
の温度変化を再現できる.
次にある点での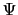 が
が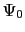 と違った値をとったと考える.そのとき
と違った値をとったと考える.そのとき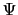 は空間的にどのように変化するであろうか.(7.5.4)式で
は空間的にどのように変化するであろうか.(7.5.4)式で
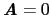 とおき,
とおき,
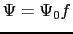 とおくと
とおくと
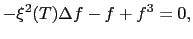 |
|
|
(7.5.31) |
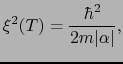 |
|
|
(7.5.32) |
となる.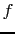 の空間的な変化の仕方は
の空間的な変化の仕方は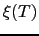 によって決まり,
によって決まり,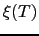 が温度
が温度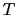 におけるコヒーレンス長になる.(7.5.11)式より
におけるコヒーレンス長になる.(7.5.11)式より
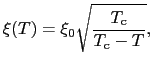 |
|
|
(7.5.33) |
と書ける.
電流の式(7.5.5)は,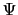 の変化の仕方が小さく,
の変化の仕方が小さく,
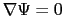 とおけるときは,
とおけるときは,
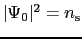 とおいて
とおいて
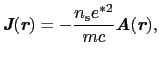 |
|
|
(7.5.34) |
となる.これの両辺のrotをとったものがロンドン方程式に相当する.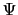 の空間変化は,だいたい
の空間変化は,だいたい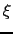 の程度の距離で起きるから,
の程度の距離で起きるから,
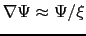 であり,これが小さいということは,
であり,これが小さいということは,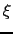 が大きいことにほかならず,第2種超伝導体の場合となる.
が大きいことにほかならず,第2種超伝導体の場合となる.
(7.5.15)式またはロンドン方程式では
という磁場の侵入距離が,磁場の変化を決める距離になっている.この
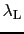 の温度変化も
の温度変化も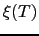 と同様に
と同様に
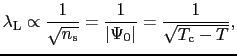 |
|
|
(7.5.35) |
の形をとる.
GL方程式は二つの特徴的な長さ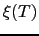 と
と
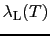 を含み,それの大小関係によって磁気的性質も変わり,第1種と第2種超伝導体との区別をもたらす.そこで
を含み,それの大小関係によって磁気的性質も変わり,第1種と第2種超伝導体との区別をもたらす.そこで
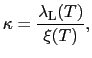 |
|
|
(7.5.36) |
というパラメーターを導入すると,これが1に比べて大きいか小さいかによって第1種と第2種とに区別されることになる.この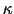 をGLパラメーターとよぶ.
をGLパラメーターとよぶ.




: BCS理論の概要
: 超伝導と遷移金属酸化物
: 完全反磁性の現象論
目次
Masashige Onoda
平成18年4月7日
![]() あるいは超伝導電子数
あるいは超伝導電子数![]() がそれに相当する.すなわち複素数である
がそれに相当する.すなわち複素数である![]() という量を考え,
という量を考え,
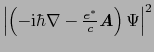 と書き換える.ここで
と書き換える.ここで
![]() を量子力学的な波動関数と考え,
を量子力学的な波動関数と考え,![]() はその点における超伝導電子の密度
はその点における超伝導電子の密度![]() に等しいと考える.磁場ゼロで電流のない場合,すなわち
に等しいと考える.磁場ゼロで電流のない場合,すなわち
![]() ,
,
![]() の場合を考える.このときは
の場合を考える.このときは![]() の場所による変化
の場所による変化
![]() であるから,そのときの
であるから,そのときの![]() を
を![]() と書くと(7.5.4)式は
と書くと(7.5.4)式は
![]() が
が![]() と違った値をとったと考える.そのとき
と違った値をとったと考える.そのとき![]() は空間的にどのように変化するであろうか.(7.5.4)式で
は空間的にどのように変化するであろうか.(7.5.4)式で
![]() とおき,
とおき,
![]() とおくと
とおくと
![]() の変化の仕方が小さく,
の変化の仕方が小さく,
![]() とおけるときは,
とおけるときは,
![]() とおいて
とおいて
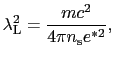
![]() と
と
![]() を含み,それの大小関係によって磁気的性質も変わり,第1種と第2種超伝導体との区別をもたらす.そこで
を含み,それの大小関係によって磁気的性質も変わり,第1種と第2種超伝導体との区別をもたらす.そこで