



: 混合状態
: 第2種超伝導体
: の決定
目次
外からの磁場をだんだん強くしていくと,第2種超伝導体では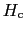 に達する前に
に達する前に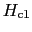 という磁場で超伝導体の中に常伝導の部分ができて,磁場はこの部分を通るようになって,内部に侵入する.そこでまず問題になるのは,この常伝導の部分はどのような形でできるかである.
という磁場で超伝導体の中に常伝導の部分ができて,磁場はこの部分を通るようになって,内部に侵入する.そこでまず問題になるのは,この常伝導の部分はどのような形でできるかである.
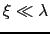 の極限の場合には,磁場の変化の様子はロンドン方程式に従うので,エネルギーの計算をすると,常伝導の部分は太さが
の極限の場合には,磁場の変化の様子はロンドン方程式に従うので,エネルギーの計算をすると,常伝導の部分は太さが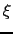 の程度の1本の線の形になることが確かめられる.すなわち直径
の程度の1本の線の形になることが確かめられる.すなわち直径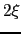 の円筒の中が常伝導になり,そこでは
の円筒の中が常伝導になり,そこでは
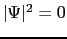 であり,外では超伝導状態で
であり,外では超伝導状態で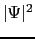 はその温度での熱平衡値
はその温度での熱平衡値
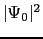 に等しい.磁場
に等しい.磁場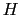 は円筒の中心で最大で,それから
は円筒の中心で最大で,それから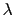 の程度離れるとゼロに近づく.
の程度離れるとゼロに近づく.
こういう線状の常伝導の部分を作るのに必要なエネルギーは,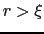 の超伝導の部分では磁場のエネルギー
の超伝導の部分では磁場のエネルギー
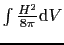 と,この磁場のために誘起される電流のための運動エネルギー
と,この磁場のために誘起される電流のための運動エネルギー
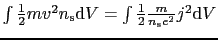 の和となり,常伝導の部分におけるエネルギーの増分は,
の和となり,常伝導の部分におけるエネルギーの増分は,
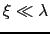 でその部分の体積が小さいから無視できる.上のエネルギーの和は,
でその部分の体積が小さいから無視できる.上のエネルギーの和は,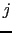 に対してマクスウェルの式を用いると
に対してマクスウェルの式を用いると
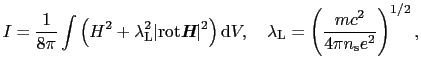 |
|
|
(7.10.59) |
と書ける.ロンドン方程式を用いて磁場
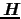 の空間変化の様子を決め,(7.10.8)式を計算すると
の空間変化の様子を決め,(7.10.8)式を計算すると
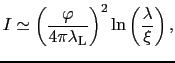 |
|
|
(7.10.60) |
となる.ただし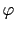 は,この常伝導の部分について入りこんだ磁束全体の値である.すなわち
は,この常伝導の部分について入りこんだ磁束全体の値である.すなわち
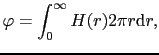 |
|
|
(7.10.61) |
で与えられる.
さてGL方程式(7.5.5)式において
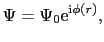 |
|
|
(7.10.62) |
とおくと,
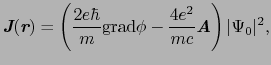 |
|
|
(7.10.63) |
と書ける.(7.10.12)式を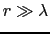 であるような大きな円周
であるような大きな円周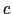 に沿って積分をする.そこでは
に沿って積分をする.そこでは
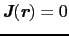 であるから
であるから
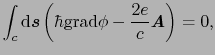 |
|
|
(7.10.64) |
となり,また第2項の積分はストークスの定理を用いて
 |
|
|
(7.10.65) |
と書ける.一方(7.10.13)式の第1項はすぐに積分でき,
![$\int_{c}{\rm grad}\phi\cdot{\rm d}\mbox{\bfseries\itshape {s}} = [\phi]$](img1381.png) は円周を1周したときの
は円周を1周したときの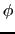 の増分に等しくなる.ところが(7.10.11)式は
の増分に等しくなる.ところが(7.10.11)式は
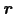 の1価関数であるから,円周を1周したとき元の値に戻らねばならない.したがって
の1価関数であるから,円周を1周したとき元の値に戻らねばならない.したがって
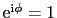 となり
となり
![$\displaystyle [\phi] = 2\pi n,\ \ \ n = 0, 1, 2, \cdots$](img1383.png) |
|
|
(7.10.66) |
となる.(7.10.14),(7.10.15)を(7.10.13)式に代入すると,超伝導体を貫く磁束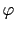 は
は
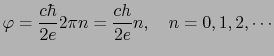 |
|
|
(7.10.67) |
というとびとびの値しかとれないことがわかる.言い換えれば,磁束は
![$\displaystyle \varphi_{0} = \frac{ch}{2e} = 2\times10^{-7}\ [{\rm G cm^{2}}],$](img1385.png) |
|
|
(7.10.68) |
を単位として量子化されていることになる.これを磁束の量子化という.
(7.10.9)式の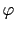 も量子化されているが,エネルギーが
も量子化されているが,エネルギーが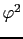 に比例しているから,
に比例しているから,
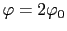 になるよりも,
になるよりも,
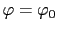 の磁束を2本作った方がエネルギーは低いことになる.つまり,外からの磁場が
の磁束を2本作った方がエネルギーは低いことになる.つまり,外からの磁場が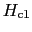 を少しこえて,磁場が超伝導体中に入り込むときは,(7.10.17)式の
を少しこえて,磁場が超伝導体中に入り込むときは,(7.10.17)式の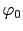 という磁束をもった1本の線として入り込むことになる.
という磁束をもった1本の線として入り込むことになる.
次にこの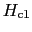 の値がどのくらいになるのかを考える.いま外から適当な磁場がかかって,超伝導体内に単位面積あたり
の値がどのくらいになるのかを考える.いま外から適当な磁場がかかって,超伝導体内に単位面積あたり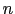 本の磁束線ができたとする.
本の磁束線ができたとする.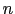 が十分小さくて,磁束線の間の相互作用を考えなくてよいときは,磁束線を作るのに必要なエネルギーは(7.10.9)式の
が十分小さくて,磁束線の間の相互作用を考えなくてよいときは,磁束線を作るのに必要なエネルギーは(7.10.9)式の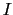 の
の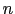 倍である.一方,このときの磁束密度は
倍である.一方,このときの磁束密度は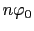 になるから,磁気的なエネルギーは
になるから,磁気的なエネルギーは
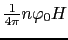 だけ下がる.すなわち全体としては
だけ下がる.すなわち全体としては
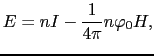 |
|
|
(7.10.69) |
となる.これは全体として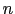 に比例するから
に比例するから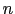 の係数が負になれば,こういう磁束線がどんどんできることになる.すなわち
の係数が負になれば,こういう磁束線がどんどんできることになる.すなわち
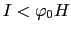 のときは,
のときは,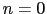 より
より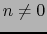 の方がエネルギーが低く,磁束線が数多くできることになる.ただし
の方がエネルギーが低く,磁束線が数多くできることになる.ただし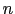 が大きくなると,磁束線の間に相互作用が働くので,
が大きくなると,磁束線の間に相互作用が働くので,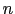 は有限の値に抑えられる.いずれにせよ
は有限の値に抑えられる.いずれにせよ
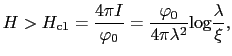 |
|
|
(7.10.70) |
になると磁束線ができはじめる.
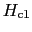 と
と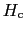 とを比べるため,
とを比べるため,
![$T = 0\ [{\rm K}]$](img1396.png) とし,
とし,
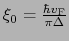 ,
,
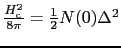 を用いると
を用いると
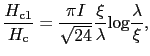 |
|
|
(7.10.71) |
となる.したがって
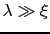 である超伝導体では,
である超伝導体では,
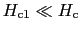 で,熱力学的な臨界磁場に達する前に,一部分が常伝導になり磁場が中に入り込むようになる.このような状態が
で,熱力学的な臨界磁場に達する前に,一部分が常伝導になり磁場が中に入り込むようになる.このような状態が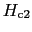 まで続き,この
まで続き,この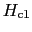 と
と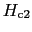 の間の状態を混合状態と呼ぶ.
の間の状態を混合状態と呼ぶ.




: 混合状態
: 第2種超伝導体
: の決定
目次
Masashige Onoda
平成18年4月7日
![]() の超伝導の部分では磁場のエネルギー
の超伝導の部分では磁場のエネルギー
![]() と,この磁場のために誘起される電流のための運動エネルギー
と,この磁場のために誘起される電流のための運動エネルギー
![]() の和となり,常伝導の部分におけるエネルギーの増分は,
の和となり,常伝導の部分におけるエネルギーの増分は,
![]() でその部分の体積が小さいから無視できる.上のエネルギーの和は,
でその部分の体積が小さいから無視できる.上のエネルギーの和は,![]() に対してマクスウェルの式を用いると
に対してマクスウェルの式を用いると
![]() も量子化されているが,エネルギーが
も量子化されているが,エネルギーが![]() に比例しているから,
に比例しているから,
![]() になるよりも,
になるよりも,
![]() の磁束を2本作った方がエネルギーは低いことになる.つまり,外からの磁場が
の磁束を2本作った方がエネルギーは低いことになる.つまり,外からの磁場が![]() を少しこえて,磁場が超伝導体中に入り込むときは,(7.10.17)式の
を少しこえて,磁場が超伝導体中に入り込むときは,(7.10.17)式の![]() という磁束をもった1本の線として入り込むことになる.
という磁束をもった1本の線として入り込むことになる.
![]() の値がどのくらいになるのかを考える.いま外から適当な磁場がかかって,超伝導体内に単位面積あたり
の値がどのくらいになるのかを考える.いま外から適当な磁場がかかって,超伝導体内に単位面積あたり![]() 本の磁束線ができたとする.
本の磁束線ができたとする.![]() が十分小さくて,磁束線の間の相互作用を考えなくてよいときは,磁束線を作るのに必要なエネルギーは(7.10.9)式の
が十分小さくて,磁束線の間の相互作用を考えなくてよいときは,磁束線を作るのに必要なエネルギーは(7.10.9)式の![]() の
の![]() 倍である.一方,このときの磁束密度は
倍である.一方,このときの磁束密度は![]() になるから,磁気的なエネルギーは
になるから,磁気的なエネルギーは
![]() だけ下がる.すなわち全体としては
だけ下がる.すなわち全体としては
![]() と
と![]() とを比べるため,
とを比べるため,
![]() とし,
とし,
![]() ,
,
![]() を用いると
を用いると