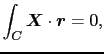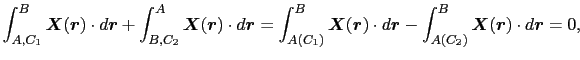: ベクトル積と回転
: 静電ポテンシャル
: 静電ポテンシャル
ストークスの定理は線積分を面積分に変換する定理で,前述のガウスの定理と並んで電磁気学において最もよく利用される数学上の定理である.すなわち,次の任意のベクトル場 (
( ),
),
を考えたとき,
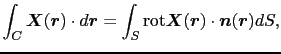 |
|
|
(1.4.58) |
の関係が成り立つ.
図 1.15:
閉曲線 によって囲まれた曲面
によって囲まれた曲面
|
|
左辺の線積分は任意の閉曲線 に関して一周にわたる積分であり,図1.15のように右辺の積分は閉曲線
に関して一周にわたる積分であり,図1.15のように右辺の積分は閉曲線 によって囲まれる任意の曲面
によって囲まれる任意の曲面 上での面積分である.rotはローテーション(rotation;回転)と呼ばれる演算子である.rot
上での面積分である.rotはローテーション(rotation;回転)と呼ばれる演算子である.rot 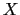 (
( )の成分は,
)の成分は,
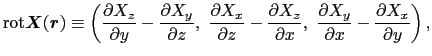 |
|
|
(1.4.59) |
で与えられる. (
( )は曲面
)は曲面 上の点
上の点 で
で に垂直に立てた単位ベクトルである.
に垂直に立てた単位ベクトルである.
(1.4.3)式の定理を二次元の平面曲線 と,それによって囲まれる平面領域
と,それによって囲まれる平面領域 上で証明してみよう.
上で証明してみよう.
確かにストークスの定理が成り立っている.
次に図1.17のように,平面上の線積分を任意の平面曲線 の一回りにわたって計算してみよう.このときには,閉曲線により取り囲まれる平面を微小な正方形に分割して考えればよい.隣り合わせの正方形上の線積分の方向は反対向きになっており,そのためこの部分の線積分は相殺し,隣り合う相手のない周辺上の線積分だけが残るため,
の一回りにわたって計算してみよう.このときには,閉曲線により取り囲まれる平面を微小な正方形に分割して考えればよい.隣り合わせの正方形上の線積分の方向は反対向きになっており,そのためこの部分の線積分は相殺し,隣り合う相手のない周辺上の線積分だけが残るため,
となる.ここで は閉曲線
は閉曲線 により囲まれる平面領域である.成分で書くと,
により囲まれる平面領域である.成分で書くと,
となる.
ストークスの定理(1.4.3)式から,rot
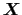 (
(
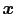 ) = 0のとき,
) = 0のとき,
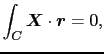 |
|
|
(1.4.60) |
の関係が導かれる.そこで,閉曲線 のまわりの一周の線積分を,A点から出発してB点に至る二つの曲線
のまわりの一周の線積分を,A点から出発してB点に至る二つの曲線
 と
と
 上の線積分に分解すると,
上の線積分に分解すると,
より,
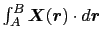 は,その途中の道筋によらず一定の値をとることがわかる.すなわち,二点間の線積分が途中の道筋によらず一定の値をとるための必要十分条件は,
は,その途中の道筋によらず一定の値をとることがわかる.すなわち,二点間の線積分が途中の道筋によらず一定の値をとるための必要十分条件は,
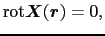 |
|
|
(1.4.61) |
で与えられる.



: ベクトル積と回転
: 静電ポテンシャル
: 静電ポテンシャル
Masashige Onoda
平成18年4月15日
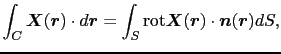
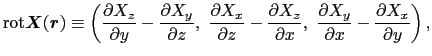
![]() と,それによって囲まれる平面領域
と,それによって囲まれる平面領域![]() 上で証明してみよう.
上で証明してみよう.
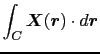
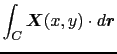
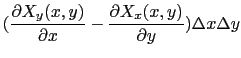
![]() の一回りにわたって計算してみよう.このときには,閉曲線により取り囲まれる平面を微小な正方形に分割して考えればよい.隣り合わせの正方形上の線積分の方向は反対向きになっており,そのためこの部分の線積分は相殺し,隣り合う相手のない周辺上の線積分だけが残るため,
の一回りにわたって計算してみよう.このときには,閉曲線により取り囲まれる平面を微小な正方形に分割して考えればよい.隣り合わせの正方形上の線積分の方向は反対向きになっており,そのためこの部分の線積分は相殺し,隣り合う相手のない周辺上の線積分だけが残るため,
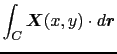
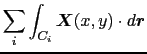
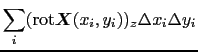
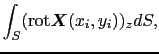
![$\displaystyle \int_{C} [X_{x}(x, y)dx + X_{y}(x, y)dy]
=
\int_{S} ({\partial X_{y}(x, y)\over{\partial x}} - {\partial X_{x}(x, y)\over{\partial y}})dS,$](img269.png)
![]() (
(
![]() ) = 0のとき,
) = 0のとき,